进制转化
十进制转 进制
例如
|666
n L_______
| 666/n -> 666 % n
n L_________
| 666/n/n -> (666/n) % n
L__________
| ....
n L__________ -> ...
| 0
n L________ -> 结束
结果是 从下往上写
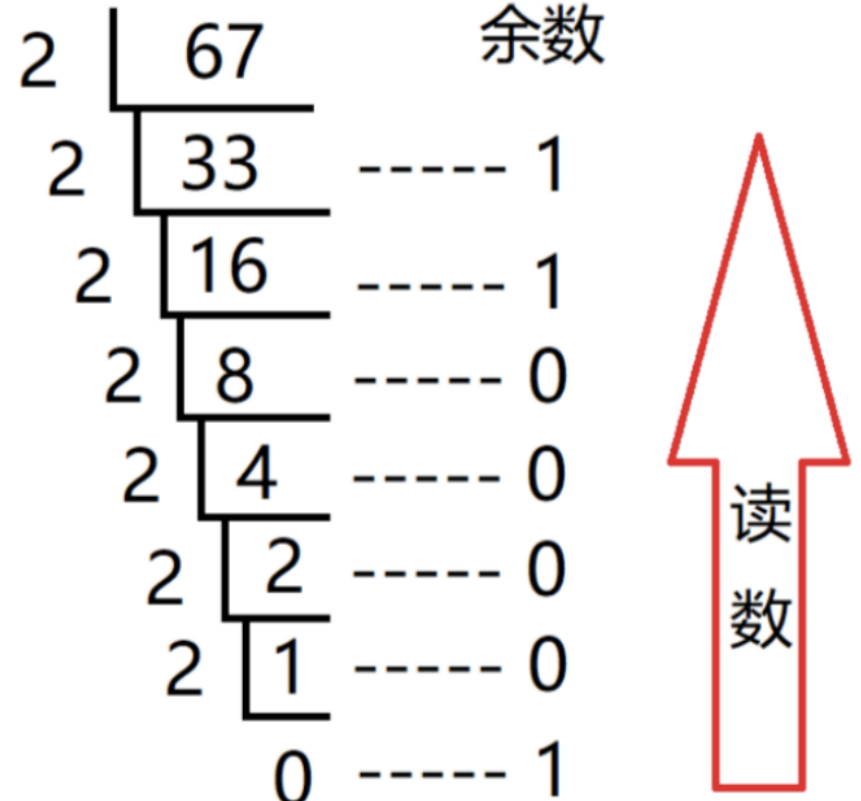
要将一个十进制数转换为 x 进制数,可以使用短除法。具体步骤如下:
- 用 x 除以该十进制数,得到商和余数。
- 将余数记录下来,将商作为新的十进制数。
- 如果商不为 0,重复步骤 1 和 2,直到商为 0,此时余数的倒序排列就是所求的 x 进制数。
以 转换为 8 进制数为例:
666 ÷ 8 = 83 ... 2
83 ÷ 8 = 10 ... 3
10 ÷ 8 = 1 ... 2
1 ÷ 8 = 0 ... 1
因此, 。
对于小数的转换,可以将小数部分单独进行转换。具体步骤如下:
将小数部分乘以 ,得到整数部分和余数。
将余数记录下来,将整数部分作为新的小数部分。
如果小数部分为 或已经达到所需精度,转换结束,余数的正序排列就是小数部分的 进制表示。
以 转换为 8 进制数为例:
将小数部分 0.666 乘以 8,得到 5.328,整数部分为 5,余数为 0.328。
将余数 0.328 乘以 8,得到 2.624,整数部分为 2,余数为 0.064。
将余数 0.064 乘以 8,得到 0.512,整数部分为 0,余数为 0.512。
小数部分为 0.526,精度已达到所需,转换结束。
| ##container## |
|---|
 |
十进制转 进制 ( ), 并且需要使用ABC..EF表示 10,12..15
#include <cstdio>
#include <algorithm>
#include <string>
using namespace std;
int main() {
string str = "0123456789ABCDEF";
long long x;
long long jz;
scanf("%lld %lld", &x, &jz);
string res;
while (x) {
res.push_back(str[x % jz]);
x /= jz;
}
reverse(res.begin(), res.end());
printf("%s\n", res.c_str());
return 0;
}
10进制转-2进制:
代码:
class Solution {
// 需要保证 k != 0
string baseK(int N, int K) {
if (!N)
return "0";
std::string res;
while (N) {
int r = N % K; // 获取余数
if (r < 0) // 保证余数为正数
r = (r + abs(K)) % abs(K);
res = std::to_string(r) + res; // 前加就无需翻转
N = (N - r) / K; // 使得其整除, 而不是向零取整
}
return std::move(res);
}
public:
string baseNeg2(int x) {
return std::move(baseK(x, -2));
}
};
进制转十进制
方法: 把 进制数按权展开、相加即得十进制
示例: 用 1001 分别以二进制、八进制、十六进制转成十进制
-
二进制 1001 转十进制
-
八进制 1001 转十进制
-
十六进制 1001 转十进制
对于小数, 则是
输入一个 进制数, 把它转化为 十进制!
#include <iostream>
#include <string>
using namespace std;
int main() {
string str;
int jz;
cin >> str >> jz;
long long res = 0;
long long k = 1;
for (int i = str.size() - 1; i >= 0; --i) {
if ('0' <= str[i] && str[i] <= '9') {
res += (str[i] - '0') * k;
} else {
res += (10 + str[i] - 'A') * k;
}
k *= jz; // 类似于快速幂的思想
}
cout << res << endl;
return 0;
}
进制转 进制
一般以10进制作为中间桥梁, 但是C++需要高精度, 所以摊牌了, 再见!
#include <iostream>
#include <string>
using namespace std;
int main() {
// 构造映射
string ys = "0123456789";
{
string tmp;
for (int i = 0; i < 26; ++i) {
ys += 'A' + i;
tmp += 'a' + i;
}
ys += tmp;
}
int x, y;
string s;
cin >> x >> y >> s; // x 进制的 s 转化为 y 进制
long long k = 1;
long long jg = 0;
string res;
for (int i = s.size() - 1; i >= 0; --i) {
if ('0' <= s[i] && s[i] <= '9') {
jg += (s[i] - '0') * k;
} else if ('A' <= s[i] && s[i] <= 'Z') {
jg += (10 + s[i] - 'A') * k;
} else {
jg += (36 + s[i] - 'a') * k;
}
k *= x;
}
while (jg) {
res.push_back(ys[jg % y]);
jg /= y;
}
for (int i = res.size() - 1; i >= 0; --i)
cout << res[i];
return 0;
}

