二叉树
二叉树简介
二叉树定义
- 二叉树是每个结点最多有两个子树的树结构。二叉树不允许存在度大于2的树,
- 它有五种最基本的形态:
- 二叉树可以是空集
- 根可以有空的左子树或者右子树;
- 左右子树都是空。只有左子树或者右子树的叫做斜树。
| ##container## |
|---|
 |
二叉树的概念和性质
满二叉树与完全二叉树
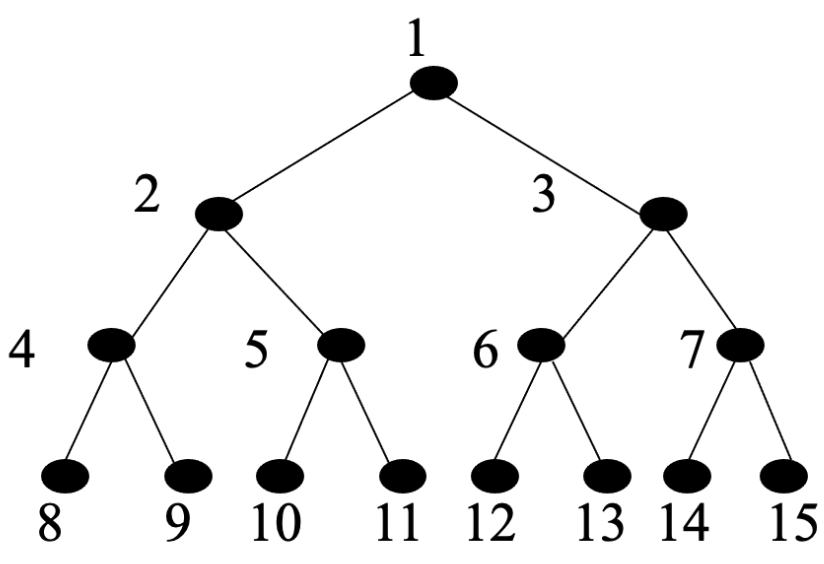
满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都 在同一层上,这样的二叉树称为满二叉树。
一棵深度为 且有 个结点的二叉树称为满二叉树。
| ##container## |
|---|
 |
完全二叉树
如果一棵深度为
k,有n个结点的二叉树中各结点能够与深度为k的顺序编号的满二叉树从1到n标号的结点相对应的二叉树称为完全二叉树。
| ##container## |
|---|
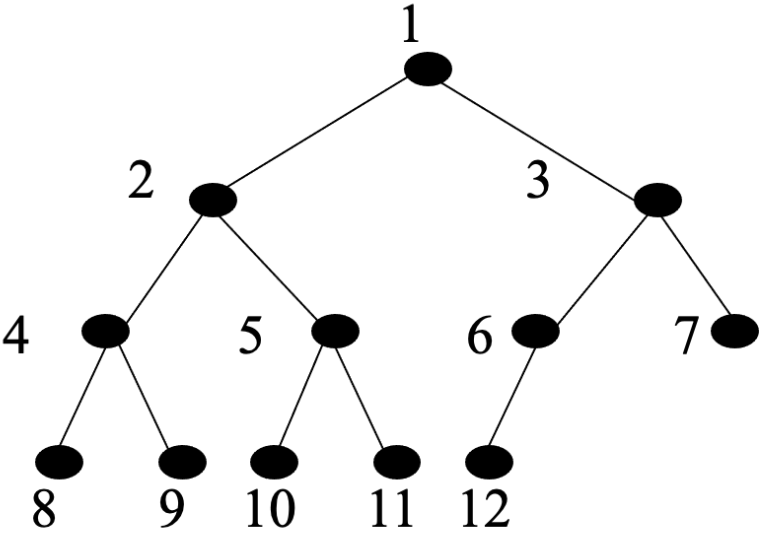 |
特点
- 所有的叶结点都出现在第
k层或者第k-1层. - 若任一结点,如果其右子树的最大层次为
i,则其左子树的最大层次为i或i+1.
二叉树的性质
- 性质1:
在二叉树的第
i层上的结点最多为 个. (i >= 1) - 性质2:
深度为k的二叉树至多有 个结点. (i ≥ 1)
- 性质3:
在一棵二叉树中,叶结点的数目比度为
2的结点数目多一个。a. 总节点数为各类节点之和:
b. 总节点数为所有子节点数加一:
故:
- 性质4:
具有N个结点的完全二叉树的深度为 。(向下取整)
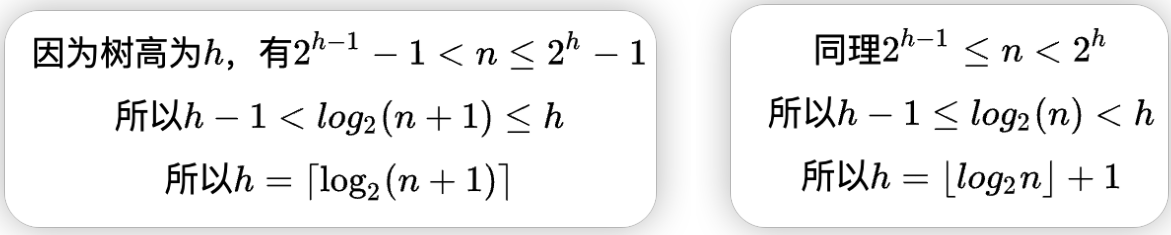
- 性质5:
如果有一棵n个结点的完全二叉树,其结点编号按照层次序(从上到下,从左到右),则除根结点(没有父结点)外,满足
[i/2,i, 2i, 2i+1]的规则即
[父结点, 自己, 左孩子, 右孩子]
二叉树的存储
顺序存储
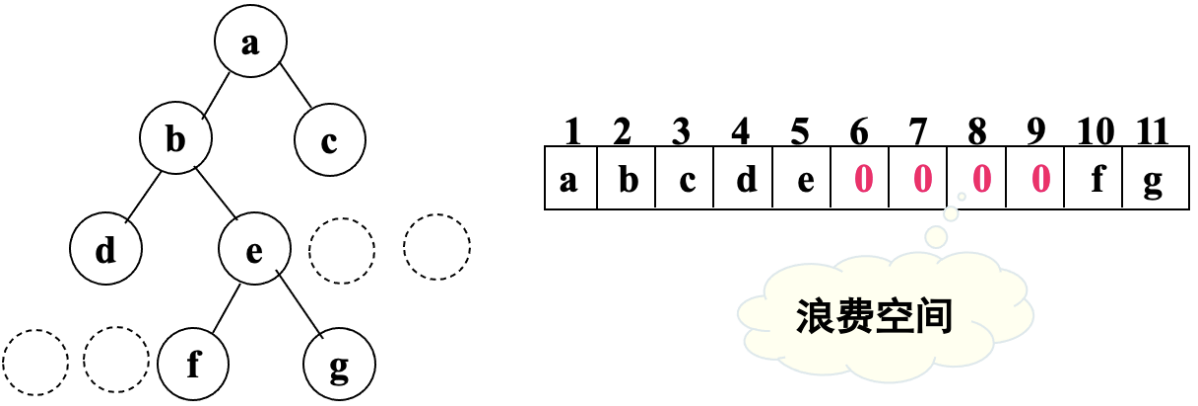
- 依靠
性质5,可以将任意棵二叉树构造成满二叉树结构或完全二叉树结构,依据下标规则,就可以找到父结点,子结点。
| ##container## |
|---|
 |
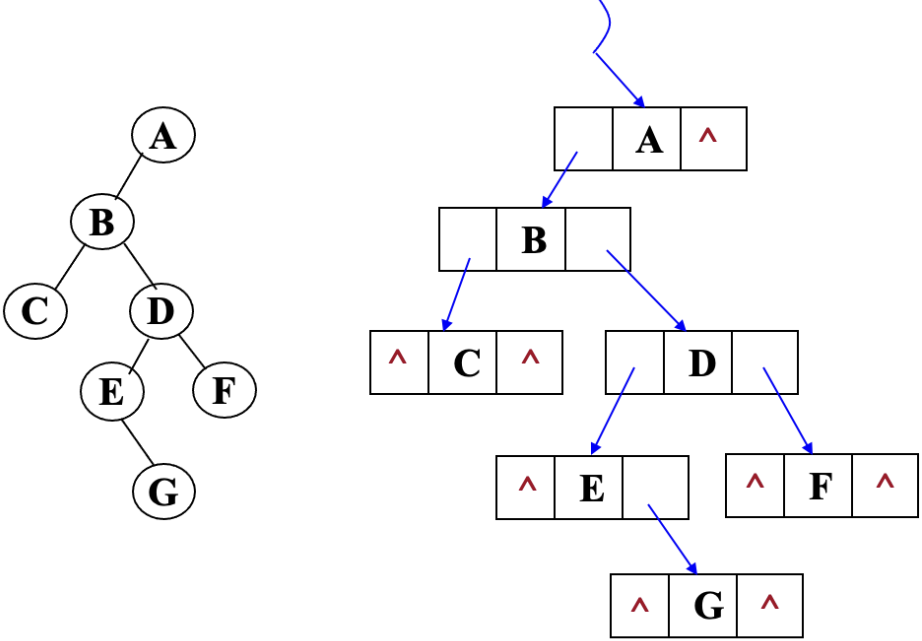
链式存储
- 由于二叉树的每个结点最多只能有两个子树,每个结点定义两个指针域和一个数据域即可.
| ##container## |
|---|
 |
二叉树的遍历
遍历思想
- 遍历:沿某条搜索路径周游二叉树,对树中的每一个节点访问一次且仅访问一次。
- 对线性结构而言,只有一条搜索路径(因为每个结点均只有一个后继),故不需要另加讨论。
- 二叉树是非线性结构,每个结点有两个后继,则存在如何遍历即按什么样的搜索路径进行遍历的问题。
- 按层次,父子关系,知道了父,那么就把其所有的子结点都看一遍
- 按深度,一条道走到黑,然后再返回走另一条道
| ##container## |
|---|
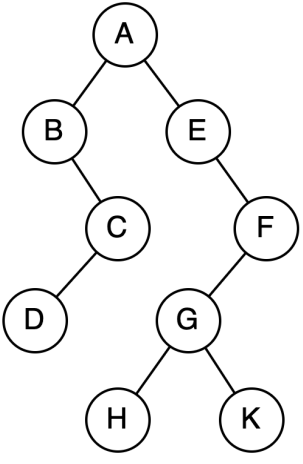 |
遍历结果:
(中左右) 前序遍历: A B C D E F G H K
(左中右) 中序遍历: B D C A E H G K F
(左右中) 后序遍历: D C B H K G F E A
广度遍历
- 算法思想
- 引入队列,将根结点入队
- 从队列中取出队头元素,访问该结点,将该结点的所有孩子节点入队
- 再次从队列中取出队头元素,并访问,以此重复
- 直到队列为空,说明所有元素都遍历完成
- 算法实现
递归
递归的概念
- 递归其实就是某个函数直接或者间接的调用了自身。这种调用方式叫递归调用。说白了还是一个函数调用。
- 既然是函数调用,那么就有一个雷打不动的原则:所有被调用的函数都将创建一个副本,各自为调用者服务,而不受其他函数的影响。
递归的条件
递归函数分为两个条件,边界条件和递归条件。
- 边界条件:就是递归中止条件,避免出现死循环。也叫做递归出口。
- 递归条件:也就是递归体。将一个大问题分解为一步步小问题。也是递归调用的阶段。
递归函数在具备这两个要素以后,才可以在有限次的计算后得出想要的结果。
深度遍历
前序遍历
中序遍历
后序遍历
代码实现: 二叉树的前中后层遍历code
根据遍历结果重构二叉树
- 如果某树的前序遍历结果是
abdgcefh, 中序遍历结果是dgbaechf, 问: 后序遍历结果是?
gdbehfca
- 已知一棵⼆叉树的中序序列和后序序列分别是
BDCEAFHG和DECBHGFA,请画出这棵⼆叉树
A
/ \
B F
\ \
C \
/ \ G
D E /
H

