二叉平衡树 (AVL树)
AVL树是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差的绝对值为1,因此它也被称为高度平衡树。AVL树是根据它的发明者G.M.Adelson-Velsky和E.M.Landis命名的。
查找、插入和删除在平均和最坏情况下的时间复杂度都是 。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。
二叉搜索树的问题
- 二叉搜索树的查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。
- 二叉搜索树会退化成单链表,搜索效率降低为O(n)
二叉搜索树一定程度上可以提高搜索效率,但是当原序列有序时,例如序列A={1,2,3,4, 5,6},构造二叉搜索树如图。依据此序列构造的二叉搜索树为右斜树,同时二叉树退化成单链表,搜索效率降低为 O(n)。
二叉搜索树的查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。
平衡因子
左子树与右子树的高度差即为该节点的平衡因子(BF,BalanceFactor)平衡二叉树中不存在平衡因子大于1的节点。- 在一棵平衡二叉树中,节点的平衡因子只能取
0、1或者-1,分别对应着左右子树等高,左子树比较高,右子树比较高。
AVL树失衡情况分析
LL, LR, RR, RL
LL:失衡节点左边高,新插入节点是在失衡节点左孩子的左边。直接对失衡节点进行右旋即可。RR:失衡节点右边高,新插入节点是在失衡节点右孩子的右边。直接对失衡节点进行左旋即可。LR:失衡节点左边高,新插入节点是在失衡节点左孩子的右边。先对左孩子进行左旋,再对失衡节点进行右旋。RL:失衡节点右边高,新插入节点是在失衡节点右孩子的左边。先对右孩子进行右旋,再对失衡节点进行左旋
即
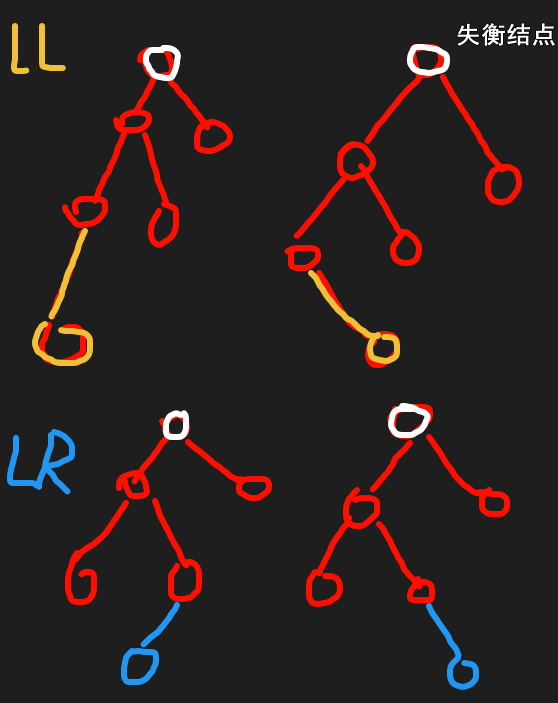
解决失衡的办法:

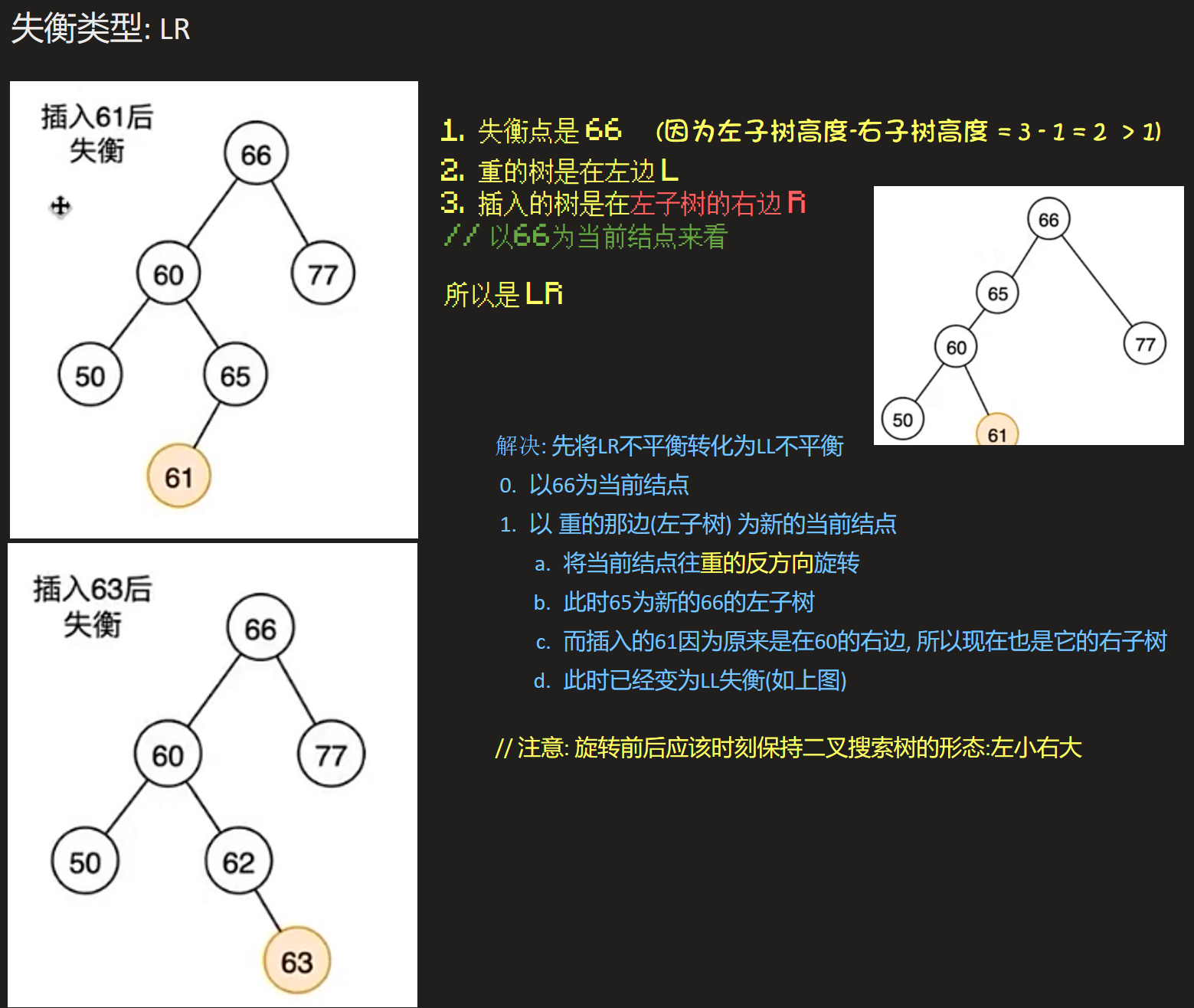
AVL树的插入操作
- 算法思路
- 先找到要插入的节点位置,插入新节点
- 更新平衡因子,根据平衡因子小于-1和大于1的情况进行讨论
平衡二叉树的删除操作
- 算法思路
- 依据二叉排序树的删除特点,依然按照3种条件进行删除,保证最后删除的都是叶子节点即可。
- 节点删除后,依次对节点进行平衡因子检查,若发现某节点不平衡,按照平衡调节法进行调节。
代码实现
判断某个结点的高度
实现AVL树, 还需要实现平衡因子的判断: 即某结点的高度
int getTreeNodeHeight(BTreeNode *T)
{
// 返回以结点T为根的数的高度
if (T)
{
int l = getTreeNodeHeight(T->left);
int r = getTreeNodeHeight(T->right);
return l > r ? l + 1 : r + 1;
}
else
{
return 0;
}
}
递归实现
#include <stdio.h>
#include <stdlib.h>
typedef int Element;
typedef struct _avlNode
{
Element data;
struct _avlNode *left;
struct _avlNode *right;
int height; // 结点高度
} AVLNode;
typedef struct
{
AVLNode *root; // 树根
int nodeNum; // 结点数
} AVLTree;
AVLTree *initAVL(void); // 初始化并返回树头
AVLNode *initAVLNode(Element e); // 返回带值的结点 问:树高计算?
AVLNode *leftRotate(AVLNode *x); // 左旋
AVLNode *rightRotate(AVLNode *y); // 右旋
void deleteAVLNode(AVLTree *T, Element e); // 删除
void putBST(AVLTree *T); // 中序遍历
void freeBinaryTree(AVLTree **T); // 释放
AVLNode *addAVLNode(AVLTree *T, AVLNode *p , Element e); // 插入结点
int getNodeHeight(AVLNode *p);
int numMax(int a, int b);
AVLTree *initAVL(void)
{
AVLTree *T = (AVLTree *)malloc(sizeof(AVLTree));
if (!T)
{
printf("malloc error!\n");
return NULL;
}
T->root = NULL;
T->nodeNum = 0;
return T;
}
AVLNode *initAVLNode(Element e)
{
AVLNode *p = (AVLNode *)malloc(sizeof(AVLNode));
if (!p)
{
printf("malloc error!\n");
return NULL;
}
p->data = e;
p->height = 1; // ?
p->left = NULL;
p->right = NULL;
return p;
}
int getNodeHeight(AVLNode *p)
{
if (p)
return p->height;
return 0;
}
int numMax(int a, int b)
{
return a > b ? a : b;
}
/* 左旋操作
* px px
* | |
* x y
* / \ ---> / \
* lx y x ry
* / \ / \
* ly ry lx ly
* 记得要更新高度: x, y的
* 其他结点不用更新, 因为没有接入新的结点, 所以相对高度没有变化
* */
AVLNode *leftRotate(AVLNode *x)
{
AVLNode *y = x->right;
x->right = y->left;
y->left = x;
// 小心不能为空
// 注意顺序: 如果先更新y再更新x, 会因为y判断左子树(x)而x又没有更新, 导致数据不正确!
x->height = numMax(getNodeHeight(x->left) + 1, getNodeHeight(x->right) + 1);
y->height = numMax(getNodeHeight(y->left) + 1, getNodeHeight(y->right) + 1);
return y;
}
/* 右旋操作
* py py
* | |
* y x
* / \ ---> / \
* x ry lx y
* / \ / \
* lx rx rx ry
* */
AVLNode *rightRotate(AVLNode *y)
{
AVLNode *x = y->left;
y->left = x->right;
x->right = y;
y->height = numMax(getNodeHeight(y->left) + 1, getNodeHeight(y->right) + 1);
x->height = numMax(getNodeHeight(x->left) + 1, getNodeHeight(x->right) + 1);
return x;
}
AVLNode *addAVLNode(AVLTree *T, AVLNode *p, Element e)
{
// 1. 找位置
if (p)
{
if (p->data > e)
{
p->left = addAVLNode(T, p->left, e);
p->height = numMax(p->height, getNodeHeight(p->left) + 1);
}
else if (p->data < e)
{
p->right = addAVLNode(T, p->right, e);
p->height = numMax(p->height, getNodeHeight(p->right) + 1);
}
else
{
// 不接受相同的数字
printf("[错误]: 插入的数字: %d 已存在!\n", e);
return p; // 注意! 递归返回赋值要返回自己!, 不是返回NULL!
}
}
else
{
++T->nodeNum;
return initAVLNode(e);
}
// 3. 计算 平衡因子 == 左子树高 - 右子树高, 并且进行旋转
if (getNodeHeight(p->left) - getNodeHeight(p->right) > 1)
{
// L?
if (getNodeHeight(p->left->left) < getNodeHeight(p->left->right)) // LR (左子树左旋)
p->left = leftRotate(p->left);
// 右旋
return rightRotate(p);
}
else if (getNodeHeight(p->left) - getNodeHeight(p->right) < -1)
{
// R?
if (getNodeHeight(p->right->left) > getNodeHeight(p->right->right)) // RL (右子树右旋)
p->right = rightRotate(p->right);
return leftRotate(p);
}
return p;
}
static AVLNode *_deleteAVLNode(AVLTree *T, AVLNode *node, Element e)
{
// 0. 退出条件: <查找元素不在AVLTree>
if (!node)
return node;
// 1. 递归查找
if (node->data > e)
{
node->left = _deleteAVLNode(T, node->left, e);
}
else if (node->data < e)
{
node->right = _deleteAVLNode(T, node->right, e);
}
else
{
// 2. 找到该元素, 对其进行删除
// AVL树的删除与普通平衡二叉树的无异
if (!node->left || !node->right)
{
// 度为 0 或者 1
AVLNode *tmp = node->left ? node->left : node->right;
free(node);
--T->nodeNum;
return tmp; // 可以直接不需要调整高度/旋转是因为下面本身(原本)就已经是平衡的!
}
else
{
// 度为2, 转移矛盾
// 找后继结点
AVLNode *tmp = node->right;
AVLNode *p = NULL;
while (tmp->left)
{
p = tmp;
tmp = tmp->left;
}
AVLNode *cecha = tmp->right;
node->data = cecha->data;
if (p)
{
p->left = cecha;
free(tmp);
--T->nodeNum;
return node;
}
else
{
node->right = tmp->right;
free(tmp);
--T->nodeNum;
return node;
}
}
}
// 3. 更新当前结点的高度
node->height = numMax(getNodeHeight(node->left), getNodeHeight(node->right));
// 4. 对 归的平衡因子进行判断, 旋转
if (getNodeHeight(node->left) - getNodeHeight(node->right) > 1)
{
// L?
if (getNodeHeight(node->left->left) < getNodeHeight(node->left->right)) // LR (左子树左旋)
node->left = leftRotate(node->left);
// 右旋
return rightRotate(node);
}
else if (getNodeHeight(node->left) - getNodeHeight(node->right) < -1)
{
// R?
if (getNodeHeight(node->right->left) > getNodeHeight(node->right->right)) // RL (右子树右旋)
node->right = rightRotate(node->right);
return leftRotate(node);
}
return node;
}
void deleteAVLNode(AVLTree *T, Element e)
{
T->root = _deleteAVLNode(T, T->root, e);
}
static void _putBST(AVLNode *N)
{
if (N)
{
_putBST(N->left);
printf("<%d (%d)> ", N->data, N->height);
_putBST(N->right);
}
}
void putBST(AVLTree *T)
{
printf("树的结点数为: %d\n\t", T->nodeNum);
_putBST(T->root);
}
static void _freeBT(AVLNode *node)
{
if (node)
{
_freeBT(node->left);
_freeBT(node->right);
free(node);
}
}
void freeBinaryTree(AVLTree **T)
{
_freeBT((*T)->root);
free(*T);
*T = NULL;
}
void text_01(void)
{
Element data[] = {1,2,3,4,5,6,7,8,9,0};
int len = sizeof(data) / sizeof(data[0]);
AVLTree *T = initAVL();
for (int i = 0; i < len; ++i)
{
T->root = addAVLNode(T, T->root, data[i]);
}
putBST(T);
deleteAVLNode(T, 1);
putchar('\n');
putBST(T);
deleteAVLNode(T, 5);
putchar('\n');
putBST(T);
freeBinaryTree(&T);
}
int main()
{
// 平衡二叉搜索树(AVL)
text_01();
return 0;
}

