P10427 [蓝桥杯 2024 省 B] 数字接龙（疑似错题）

题目背景

本题目前未找到任何做法（在不进行特判的情况下）进行有效剪枝通过 $n = 10$，$k = 1$ 的数据。由于本题疑似错题，因此本题不提供评测以及题解区。

题目描述

小蓝最近迷上了一款名为《数字接龙》的迷宫游戏，游戏在一个大小为 $n \times n$ 的格子棋盘上展开，其中每一个格子处都有着一个 $0 \cdots k-1$ 之间的整数。游戏规则如下：

1. 从左上角 $(0,0)$ 处出发，目标是到达右下角 $(n-1,n-1)$ 处的格子，每一步可以选择沿着水平 / 垂直 / 对角线方向移动到下一个格子。
2. 对于路径经过的棋盘格子，按照经过的格子顺序，上面的数字组成的序列要满足：$0,1,2, \cdots ,k-1,0,1,2, \cdots ,k-1,0,1,2 \cdots$。
3. 途中需要对棋盘上的每个格子恰好都经过一次（仅一次）。
4. 路径中不可以出现交叉的线路。例如之前有从 $(0,0)$ 移动到 $(1,1)$，那么再从 $(1,0)$ 移动到 $(0,1)$ 线路就会交叉。

为了方便表示，我们对可以行进的所有八个方向进行了数字编号，如下图 $2$ 所示；因此行进路径可以用一个包含 $0 \cdots 7$ 之间的数字字符串表示，如下图 $1$ 是一个迷宫示例，它所对应的答案就是：$41255214$。

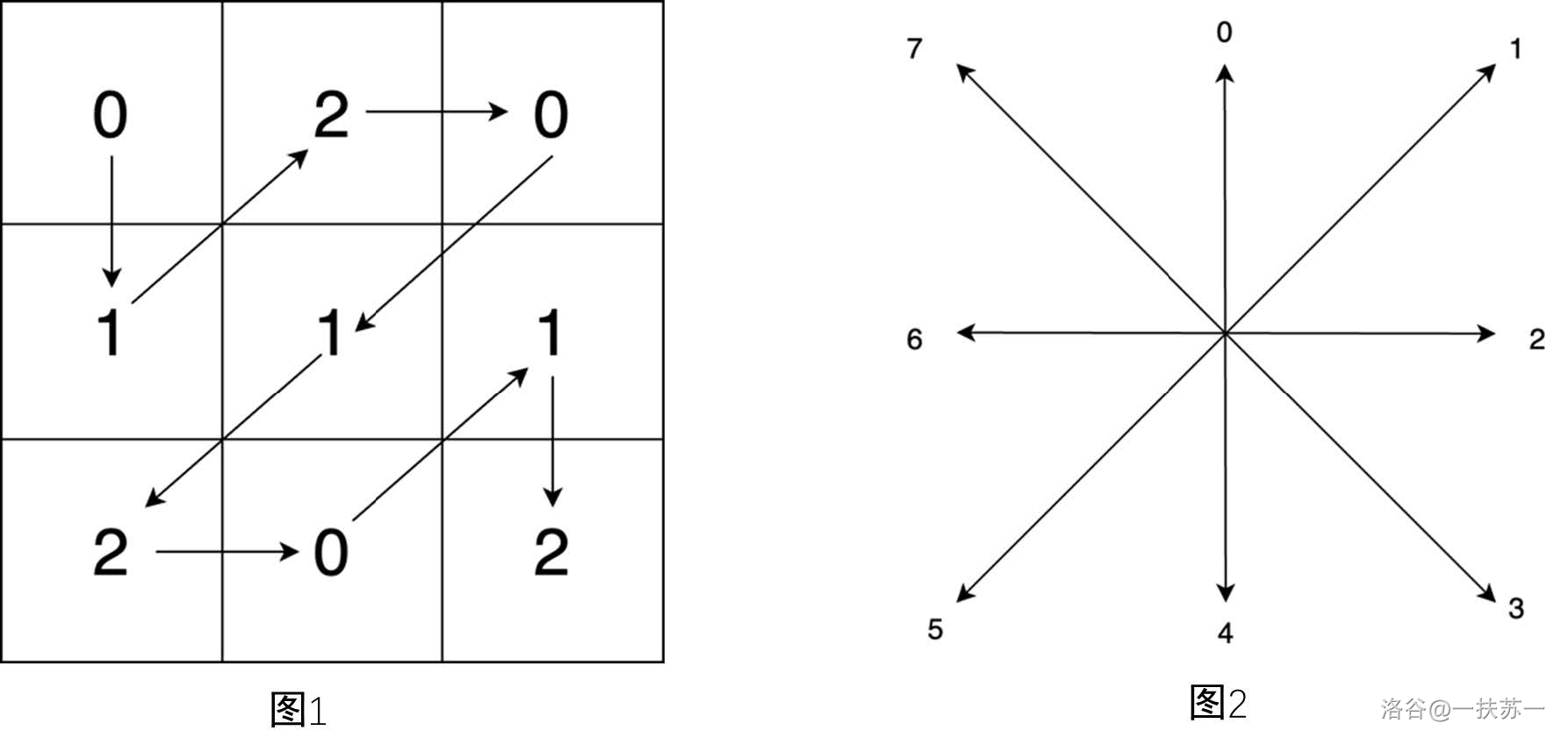
现在请你帮小蓝规划出一条行进路径并将其输出。如果有多条路径，输出字典序最小的那一个；如果不存在任何一条路径，则输出 $−1$。

输入格式

第一行包含两个整数 $n, k$。 接下来输入 $n$ 行，每行 $n$ 个整数表示棋盘格子上的数字。

输出格式

输出一行表示答案。如果没有对应的路径，输出 $-1$。

输入输出样例 #1

输入 #1

3 3
0 2 0
1 1 1
2 0 2

输出 #1

41255214

说明/提示

数据规模与约定

• 对 $80\%$ 的数据，$n \leq 5$。
• 对全部的测试数据，$1 \leq n,k \leq 10$。

我写

假设题目保证不出现不可以搜索的case, 那么应该这样写:

特别难搞的是不能交叉, 但是如果只是协向有值, 那不能判断为交叉!

因此保险的做法是记录方向: int sb[10][10][10][10];, 其中sb[i][j][y][x]表示存在 (i, j) -> (y, x)

#include <iostream>
#include <vector>
#include <string>

using namespace std;

// [y][x]
constexpr int fx[8][2] = {
    {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, 
    {1, 0}, {1, -1}, {0, -1}, {-1, -1}
};

int n = 0, k = 0;
vector<vector<int>> tizu;
vector<vector<int>> vis;
set<string> res;
string now;

int sb[10][10][10][10];

void dfs(int i, int j, int next) {
    if (i == n - 1 && j == n - 1) {
        if ((int)now.size() == n * n - 1) {
            cout << now << '\n';
            exit(0);
        }
        return;
    }
    next = (next + 1) % k;
    
    for (int d = 0; d < 8; ++d) {
        char c = '0' + d;
        int y = i + fx[d][0], x = j + fx[d][1];
        if (y < 0 || y >= n || x < 0 || x >= n || vis[y][x] || tizu[y][x] != next) {
            continue;
        }
        // [i][j] -> [y][x] 
        if (c == '1' && (sb[y+1][x][y][x-1] || sb[y][x-1][y+1][x]))
            continue;
        if (c == '3' && (sb[y-1][x][y][x-1] || sb[y][x-1][y-1][x]))
            continue;
        if (c == '5' && (sb[y-1][x][y][x+1] || sb[y][x+1][y-1][x]))
            continue;
        if (c == '7' && (sb[y+1][x][y][x+1] || sb[y][x+1][y+1][x]))
            continue;
        vis[y][x] = 1;
        sb[i][j][y][x] = 1;
        now += c;
        dfs(y, x, next);
        now.pop_back();
        sb[i][j][y][x] = 0;
        vis[y][x] = 0;
    }
}

int main() {
    cin >> n >> k;
    tizu = vector<vector<int>>(n, vector<int>(n));
    vis = vector<vector<int>>(n, vector<int>(n));
    
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j) 
            cin >> tizu[i][j];
    
    vis[0][0] = 1;
    if (tizu[0][0] == 0)
        dfs(0, 0, 0);
    cout << "-1\n";
    return 0;
}

C++