【模板】单源最短路径（弱化版）

原题: P3371 【模板】单源最短路径（弱化版）

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数 $n,m,s$，分别表示点的个数、有向边的个数、出发点的编号。

接下来 $m$ 行每行包含三个整数 $u,v,w$，表示一条 $u \to v$ 的，长度为 $w$ 的边。

输出格式

输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$。

样例 #1

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

【数据范围】
对于 $20\%$ 的数据： $1\le n \le 5$，$1\le m \le 15$；
对于 $40\%$ 的数据： $1\le n \le 100$，$1\le m \le 10^4$；
对于 $70\%$ 的数据： $1\le n \le 1000$，$1\le m \le 10^5$；
对于 $100\%$ 的数据： $1 \le n \le 10^4$，$1\le m \le 5\times 10^5$，$1\le u,v\le n$，$w\ge 0$，$\sum w< 2^{31}$，保证数据随机。

Update 2022/07/29：两个点之间可能有多条边，敬请注意。

对于真正 $100\%$ 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

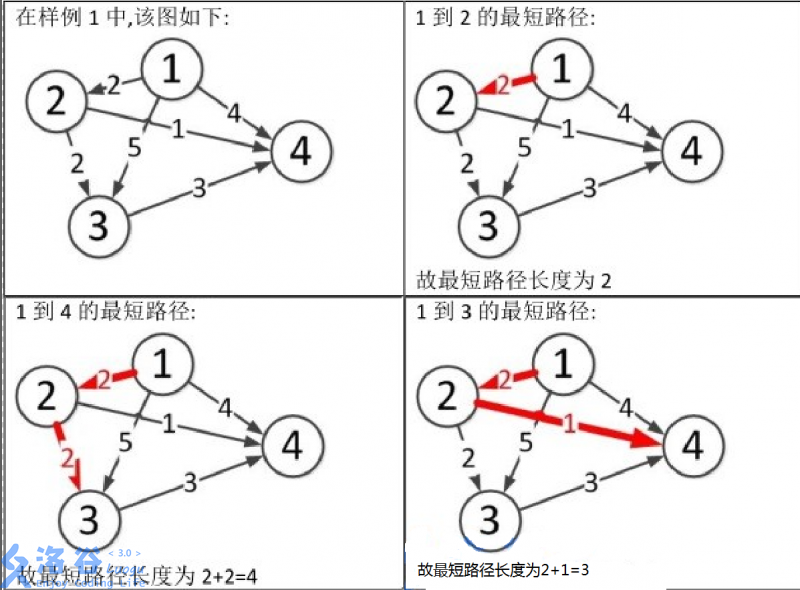
图片1到3和1到4的文字位置调换

解答

1. 因为数据量为 $10^5$, 所以存储不能使用邻接矩阵, 故需要 链式前向星: 图的存储 有介绍

2. 本题我的语文理解错了:

第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$。

指的是:

for (int i = 1; i <= n; ++i)
    printf("%d ", min_weight[i] == INF ? 2147483647 : min_weight[i]);

// 而不是
if (x == n + 1)
    for (int i = 1; i <= n; ++i)
        printf("%d ", min_weight[i]);
else
    printf("%d\n", 2147483647);

C++

代码: 迪加斯特拉算法(朴素版) 即可

#include <cstdio>
#include <vector>
using namespace std;

int main()
{
    typedef struct _e
    {
        int to;
        int next;
        int w;
    } E;
    const int INF = 2e9;
    int n, m, s;
    scanf("%d%d%d", &n, &m, &s);
    vector<E> e(m + 1, {0, 0, 0});
    vector<int> head(n + 1, 0);

    for (int i = 1, u, w, v, c; i <= m; ) {
        scanf("%d%d%d", &u, &v, &w);
        e[i].to = v;
        e[i].w = w;
        e[i].next = head[u];
        head[u] = i++;
    }

    //for (int i = 1; i <= n; ++i)
    //    for (int j = head[i]; j != 0; j = e[j].next)
    //        printf("%d -- %d --> %d\n", i, e[j].w, e[j].to);

    vector<int> min_weight(n + 1, INF);    // 距离原点最小权和
    //vector<int> parent(n + 1, -1);        // 父节点
    vector<bool> visit(n + 1, 0);        // 是否已选择

    min_weight[s] = 0;
    int x = 0;
    for (int i = s, k; ;) {
        k = 0;
        for (int j = head[i]; j != 0; j = e[j].next)
            if (!visit[e[j].to] && min_weight[i] + e[j].w < min_weight[e[j].to])
                min_weight[e[j].to] = min_weight[i] + e[j].w;


        for (int g = 1; g <= n; ++g)
            if (!visit[g] && (k == 0 || min_weight[k] > min_weight[g]))
                k = g;

        if (!k)
            break;
        i = k;
        visit[i] = 1;
    }

    for (int i = 1; i <= n; ++i) {
        printf("%d ", min_weight[i] == INF ? 2147483647 : min_weight[i]);
    }
    
    return 0;
}

C++