树
树的表达方式
集合中的元素关系呈现出一对多的情况
树的定义
- 树(Tree) 是n(n≥O)个节点的有限集合T,它满足两个条件:
- 有且仅有一个特定的称为根(Root) 的节点.
- 其余的节点可以分为m(m≥0)个互不相交的有限集合T1、T2、...、Tm,其中每一个集合又是一棵树,并称为其根的子树(Subtree).
| ##container## |
|---|
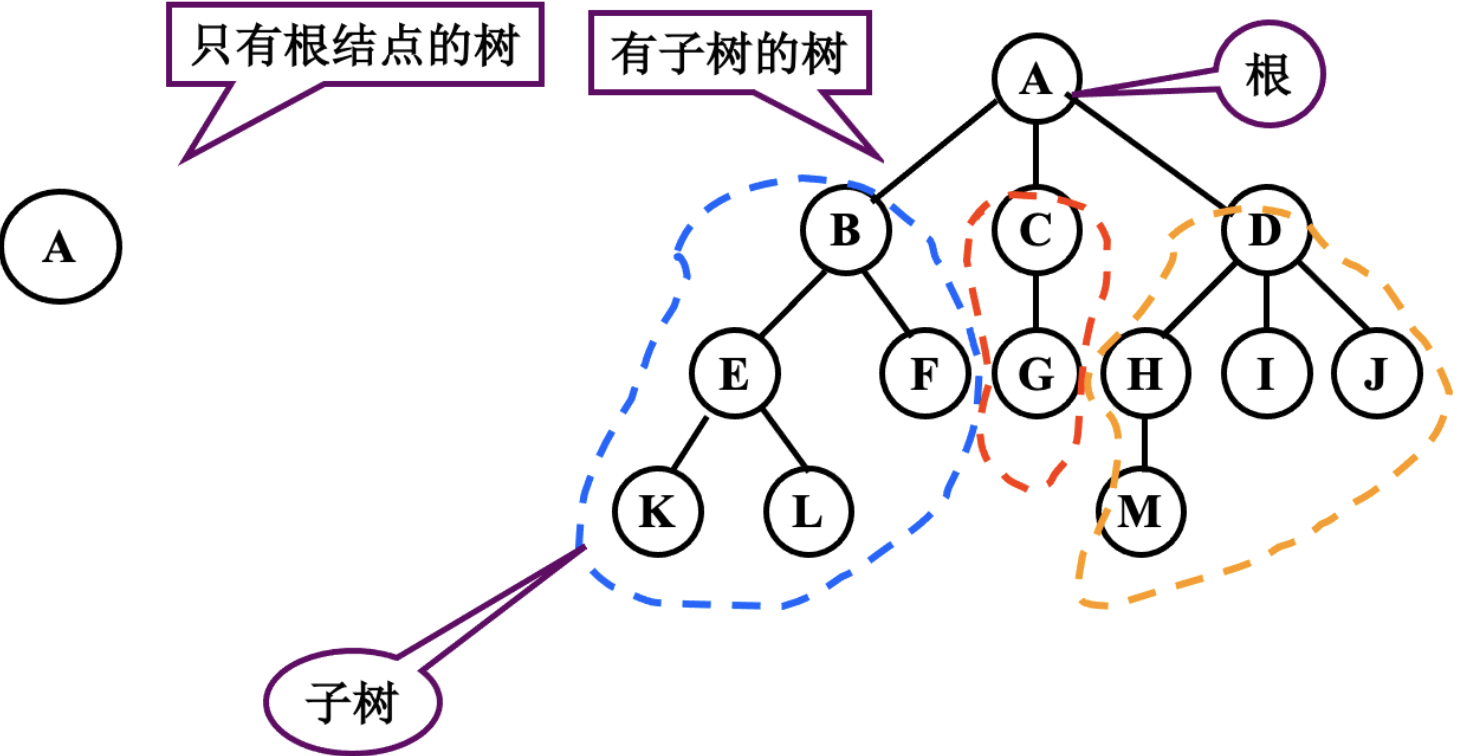 |
- 树的定义具有递归性, 即"树中还有树".
树的概念
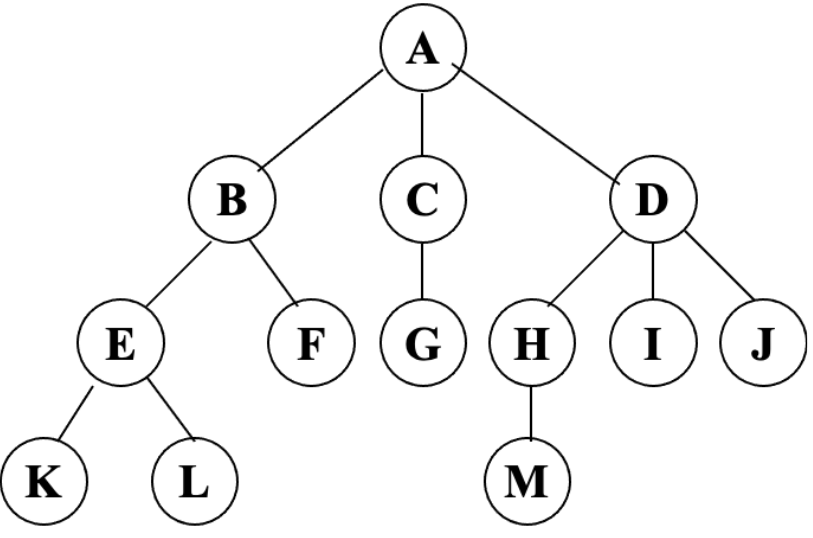
结点:使用树结构存储的每一个数据元素都被称为“结点”。例如图中的A就是一个结点。根结点:有一个特殊的结点,这个结点没有前驱,我们将这种结点称之为根结点。父结点(双亲结点)、子结点和兄弟结点:对于ABCD四个结点来说,A就是BCD的父结点,也称之为双亲结点。而BCD都是A的子结点,也称之为孩子结点。对于BCD来说,因为他们都有同一个爹,所以它们互相称之为兄弟结点。叶子结点:如果一个结点没有任何子结点,那么此结点就称之为叶子结点。结点的度:结点拥有的子树的个数,就称之为结点的度。树的度:在各个结点当中,度的最大值。为树的度。树的深度或者高度:结点的层次从根结点开始定义起,根为第一层,根的孩子为第二层。依次类推。
| ##container## | |:--:| |
|
结点A的度:3 结点B的度:2 结点M的度:0
结点A的孩子:B C D 结点B的孩子:E F
树的度:3 树的深度:4
叶子结点:K L F G M I J
结点A是结点F的祖先
结点F是结点K的叔叔结点
树的存储结构
双亲表示法
| ##container## |
|---|
 |
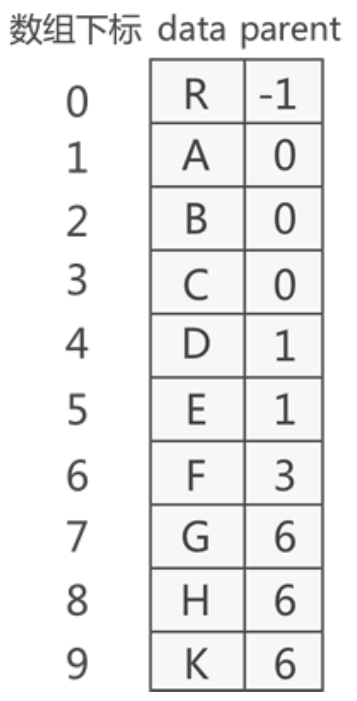
双亲表示法采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变量。
根节点没有父节点(父节点又称为双亲节点),因此根节点记录父节点位置的变量通常置
-1。
- 利用顺序表存储,表元素由数据和父结点构成
- 特点分析:
- 根结点没有双亲,所以位置域设置为
-1 - 知道一个结点,找他的父结点,非常容易,O(1)级
- 找孩子节点,必须遍历整个表
- 根结点没有双亲,所以位置域设置为
| ##container## |
|---|
 |
孩子兄弟表示法
孩子表示法存储普通树采用的是“顺序表+链表”的组合结构。
其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点。需要注意,与双亲表示法不同的是,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。
| ##container## |
|---|
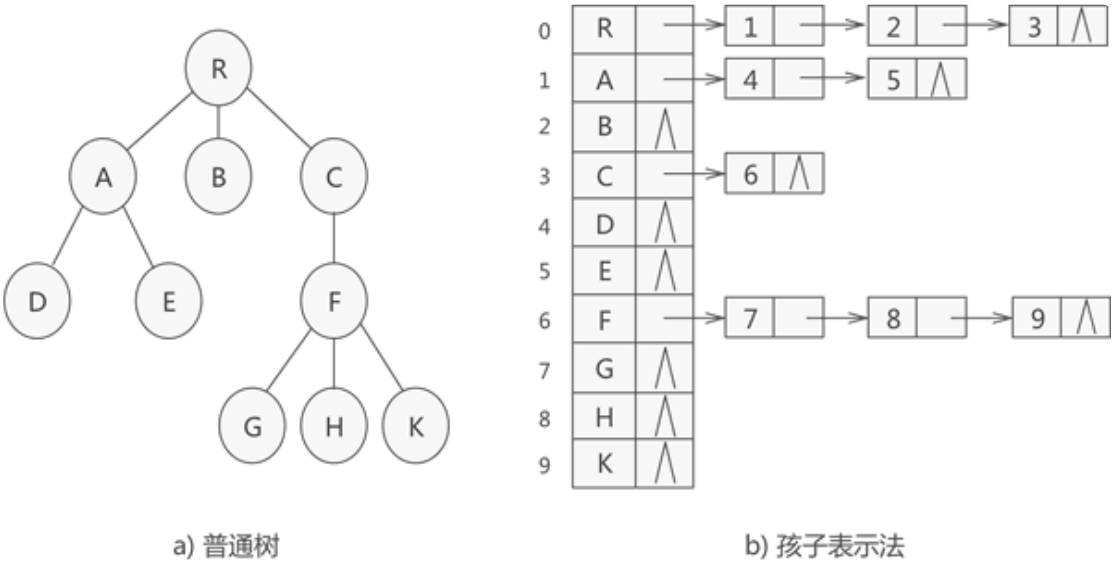 |
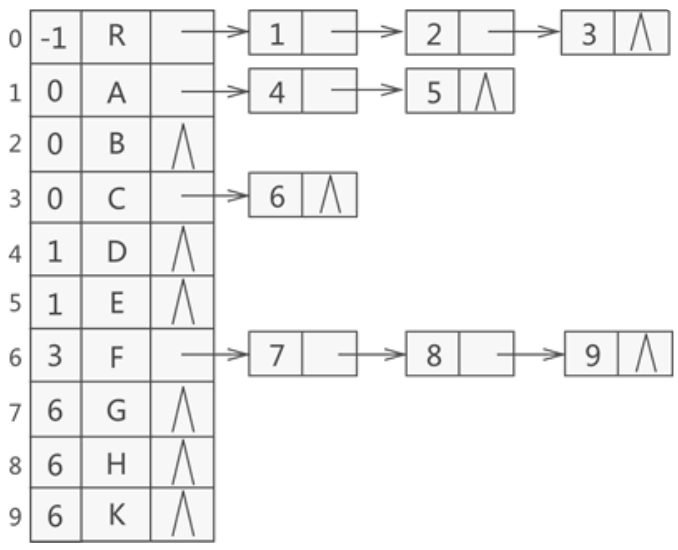
使用孩子表示法存储的树结构,正好和双亲表示法相反,查找孩子结点的效率很高,而不擅长做查找父结点的操作。
我们还可以将双亲表示法和孩子表示法合二为一:
| ##container## |
|---|
 |
孩子兄弟表示法
在树结构中,同一层的节点互为兄弟节点。例如普通树中,节点A、B 和C 互为兄弟节点,而节点D、E 和F也互为兄弟节点。
所谓孩子兄弟表示法,指的是用将整棵树用二叉链表存储起来,具体实现方案是:从树的根节点开始,依次存储各个结点的孩子结点和兄弟结点。
在二叉链表中,各个结点包含三部分内容:
| ##container## |
|---|
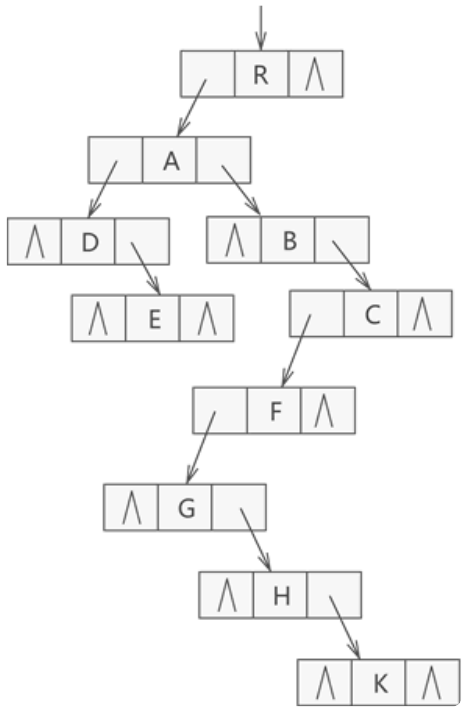 |
| 孩子兄弟表示法示例图 |
在以孩子兄弟表示法构建的二叉链表中,如果要查找结点
x的所有孩子,则只要根据该结点的firstchild指针找到它的第一个孩子,然后沿着孩子结点的nextsibling指针不断地找它的兄弟结点,就可以找到结点x的所有孩子。


