516. 最长回文子序列

原题链接: 516. 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

1 <= s.length <= 1000
s 仅由小写英文字母组成

题解

思路1 [转换]

因为是找回文序列, 即 正着读 和 反着读 是一样的, 故我们可以将s翻转, 然后就是 1143. 最长公共子序列

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        string s_2("");
        for (int i = n - 1; i >= 0; --i)
            s_2 += s[i];
        
        vector<vector<int>> dp(n + 1, vector<int>(n + 1));

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (s[i] == s_2[j])
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                else
                    dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);
            }
        }

        return dp[n][n];
    }
};
C++

思路2 [选或不选]

# 区间DP
## 区别
### 线性DP: 一般是在前/后缀上转移
### 区间DP: 从小区间转移到大区间
## 选或不选
### 从两侧向内缩小问题规模
### 本题
## 枚举选哪个
### 分割成多个规模更小的子问题
### 1039.
markmap##h300

选或不选: 从两侧向内缩小问题规模

##container##

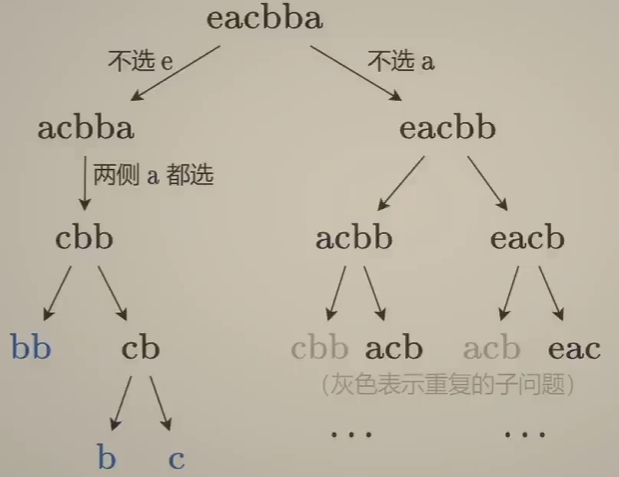故可有状态: dp[i][j] 即 s[i,...,j] 的最长回文子序列长度

思考转移:

已知 dp[i + 1][j - 1] 可以求 dp[i][j] 吗?

##container##

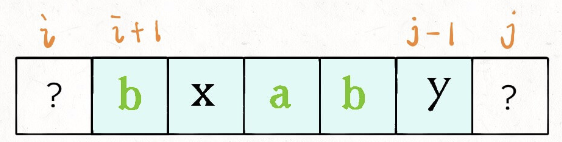显然是可以的, 即若 s[i] == s[j] 那么 dp[i][j] = dp[i + 1][j - 1] + 2;

否则, 则说明它俩不可能同时出现在 s[i..j] 的最长回文子序列中，那么把它俩分别加入 s[i+1..j-1] 中，看看哪个子串产生的回文子序列更长即可:

##container##

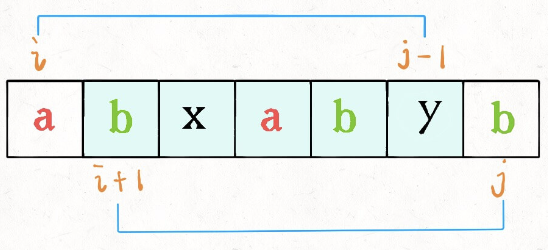代码

记忆化搜索

class Solution {
public:
    int BFS(int i, int j, string& s, vector<vector<int>>& memo) {
        if (i > j)
            return 0;

        if (i == j)
            return 1;

        if (memo[i][j])
            return memo[i][j];
        
        if (s[i] == s[j])
            memo[i][j] = BFS(i + 1, j - 1, s, memo) + 2;
        else
            memo[i][j] = max(BFS(i + 1, j, s, memo), BFS(i, j - 1, s, memo));
        
        return memo[i][j];
    }

    int longestPalindromeSubseq(string s) {
        vector<vector<int>> memo(s.size(), vector<int>(s.size()));
        return BFS(0, s.size() - 1, s, memo);
    }
};
C++

动态规划

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));

        // 值得注意的是, 遍历的顺序是 从 左下 到 右上 的
        for (int i = n - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i + 1; j < n; j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }
                else {
                    dp[i][j] = max(
                        dp[i + 1][j],
                        dp[i][j - 1]
                    );
                }
            }
        }

        return dp[0][n - 1];
    }
};
C++

对于为什么是从左下到右上的遍历:

##container##

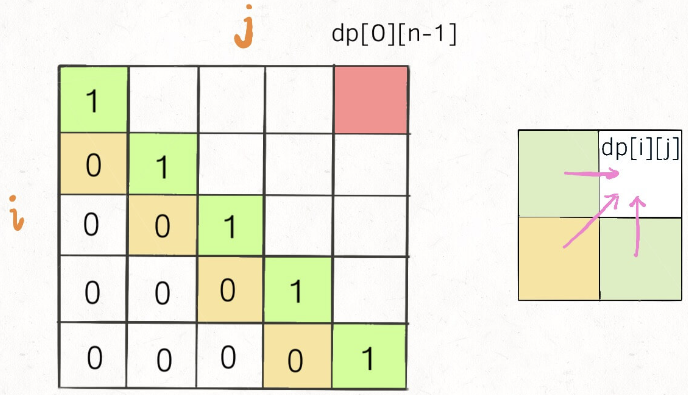如图, 并且要保证 i < j, 然后是需要优先知道`dp[i + 1][j - 1]`的数值

动态规划状态压缩至空间复杂度O(N)

不会!

示例 1：​

示例 2：​

提示：​

题解

思路1 [转换]​

思路2 [选或不选]​

代码​

记忆化搜索​

动态规划​

动态规划状态压缩至空间复杂度O(N)​

参考链接​