1976. 到达目的地的方案数

第 59 场双周赛 Q3 中等 2095

原题: 1976. 到达目的地的方案数

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有双向道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ $u_i, v_i, time_i$ ] 表示在路口 $u_i$ 和 $v_i$ 之间有一条需要花费 $time_i$ 时间才能通过的道路。你想知道花费最少时间从路口 0 出发到达路口 n - 1 的方案数。

请返回花费最少时间到达目的地的路径数目。由于答案可能很大，将结果对 1e9 + 7 取余后返回。

示例 1：

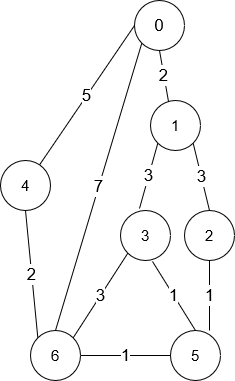
力扣的图片

输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：

0 ➝ 6
0 ➝ 4 ➝ 6
0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

提示：

$1 <= n <= 200 \\ n - 1 <= roads.length <= n * (n - 1) / 2\\ roads[i].length == 3\\ 0 <= u_i, v_i <= n - 1\\ 1 <= time_i <= 10^9\\ u_i != v_i\\ 任意两个路口之间至多有一条路。\\ 从任意路口出发，你能够到达其他任意路口。$

题解

首先我可以想到最短路径的迪加斯特拉算法, 可以求0->n-1的最短路径, 但是总觉得得使用dp, 最好是在求最短路径的过程中使用, 但是我不会...

但是我发现: 0->n-1的最短路径肯定是>= 0->i,i->n-1的最短路径的, 于是乎好像可以用弗洛伊德算法(实际上还是要dp?)

正文

使用迪加斯特拉算法!

在计算最短路的同时DP

定义 f[i] 表示节点 0 到节点i的最短路个数。

在用 dis[c] 更新 dis[y] 时:

如果 dis[c] + g[c][y] < dis[y] ，说明从 0 到 x 再到 y 的路径是目前最短的，所以更新 f[y] 为 f[x].
如果 dis[c] + g[c][y)] == dis[y] ，说明从 0 到 x 再到 y 的路径与之前找到的路径一样短，所以把f[y] 增加 f[c]。

初始值：f[0] = 1，因为 0 到 0 只有一种方案，即原地不动。

答案: f[n - 1];

class Solution {
public:
    int countPaths(int n, vector<vector<int>>& roads) {
        // 0 到 n - 1 点 的最短路径的方案数
        // n <= 200
        const long long INF = 1e18;
        const int MOD = 1e9 + 7;
        vector<vector<long long>> G(n, vector<long long>(n, INF));
        for (int i = 0; i < roads.size(); ++i) {
            G[roads[i][0]][roads[i][1]] = roads[i][2];
            G[roads[i][1]][roads[i][0]] = roads[i][2];
        }
        // 1. 求最短路径-迪加斯特拉算法
        vector<long long> minTimeByG(n, INF);
        vector<int> dp(n, 0);
        vector<bool> ifRuned(n);
        {
            dp[0] = 1; // 0 到 0 只有一种方案数, 即0到0(原地罚站)
            minTimeByG[0] = 0;
            while(1) {
                int i = -1;
                for (int j = 0; j < n; ++j) {
                    if (!ifRuned[j]) { // 为什么这里加上 && G[i][j] != INF 会答案错误
                        if (i < 0 || minTimeByG[i] > minTimeByG[j]) {
                            i = j;
                        }
                    }
                }

                if (i == n - 1)
                    break;

                ifRuned[i] = 1;
                
                for (int j = 0; j < n; ++j) {
                    long long now_len = minTimeByG[i] + G[i][j];
                    if (minTimeByG[j] > now_len) {
                        dp[j] = dp[i];
                        minTimeByG[j] = now_len;
                    }
                    else if (minTimeByG[j] == now_len) {
                        dp[j] = (dp[i] + dp[j]) % MOD;
                    }
                }
            }
        }
        // 废弃的错误思路: 先求到n-1点的最短路径
        // 然后就是一个背包问题但是必需是连续的?,
        // 容量(时间), 价值(时间)
        // 不好做
        return dp[n - 1];
    }
};
C++