堆排序
1.堆的概念
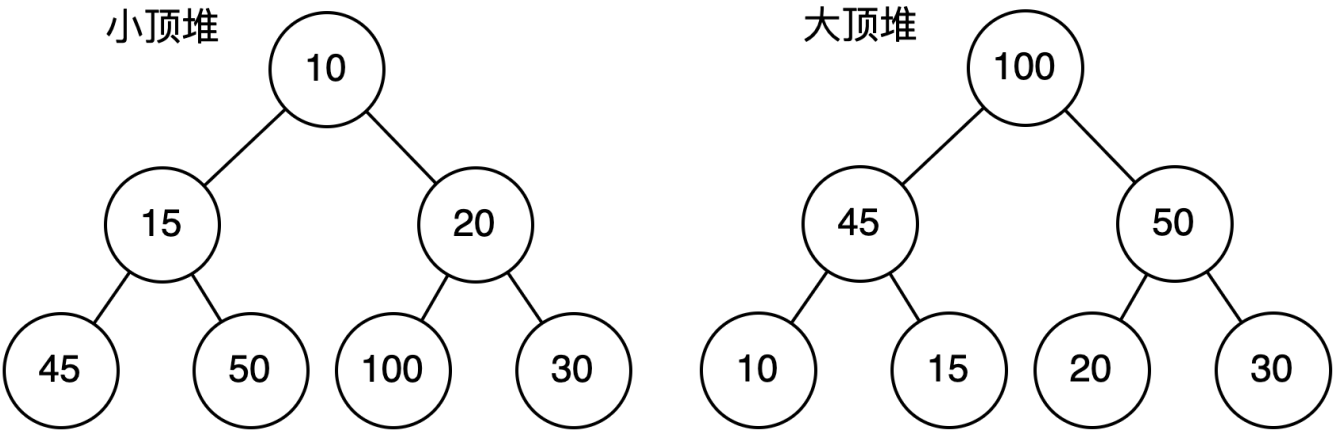
堆(Heap) 是一类基于完全二叉树的特殊数据结构。
通常将堆分为两种类型:
-
大顶堆(Max Heap):
- 在大顶堆中,根节点的值必须大于他的孩子节点的值,对于二叉树中所有子树都满足此规律;
-
小顶堆(Min Heap):
- 在小顶堆中,根节点的值必须小于他的孩子节点的值,对于二叉树中所有子树都满足此规律;
小顶堆就是以任意一个结点作为根,其左右孩子都要大于等于该节点的值,所以整颗树的根结点一定是树中值最小的节点,而大顶堆正好特性相反。
| ##container## |
|---|
 |
2. 二叉堆
2.1 二叉堆的属性
二叉堆是满足下面属性的一颗二叉树:
- 二叉堆必定是一颗完全二叉树。二叉堆的此属性也决定了他们适合存储在数组当中。
- 二叉堆要么是小顶堆,要么是大顶堆。
- 小顶二叉堆中的根结点的值是整棵树中的最小值,而且二叉树中的所有顶点及其子树均满足这一特性。
- 大顶堆与小顶堆类似,大顶堆的根节点的值是整棵树中的最大值,而且二叉树中所有结点的值也均大于等于其子树结点。
由于小顶堆和大顶堆除了在顶点的大小关系上不一致,两者均是一颗全完二叉树,下面的所有讲解,都以小顶堆为例进行说明,会了小顶堆,大顶堆你自己都能写出来。
2.2 二叉堆的存储
可以申请 个空间,从 索引开始存储,满足 的父、自己、左孩、右孩的索引关系。
3.小顶堆的常见操作
3.1初始化小顶堆
初始化顺序表,以 个数进行初始化
3.2 插入节点
当二叉堆插入节点时,插入位置是完全二叉树的最后一个位置。然后开始上移操作
3.3 获取/移除最小元素
二叉堆删除节点的过程和插入节点的过程正好相反,所删除的是处于堆顶的节点。
这时,为了继续维持完全二叉树的结构,我们把堆的最后一个节点临时补到原本堆顶的位置。
代码
如果C++的话, 可以使用STL的 优先级队列priority_queue 或者 原生(指#include <algorithm>后对存储在数组或vector中的元素进行堆操作的函数)的heap
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
typedef int Element;
// 小根堆结构体 注意索引从1开始
typedef struct {
int *data; // 数据
int size; // 最大长度
int len; // 当前长度
} BinaryHeap;
BinaryHeap *createHeap(int n); // 开辟一个大小为n的堆
void heapInsert(BinaryHeap *heap, Element e); // 往堆中插入一个元素
Element getHeapTop(BinaryHeap *heap); // 获取堆顶元素
void delHeapTop(BinaryHeap *heap); // 删除堆顶元素
void heapPrint(BinaryHeap *heap); // 打印
BinaryHeap *createHeap(int n) {
BinaryHeap *heap = (BinaryHeap *)malloc(sizeof(BinaryHeap));
heap->data = (int *)malloc(sizeof(int) * (n + 1));
if (!heap->data) {
printf("malloc failed\n");
return NULL;
}
heap->size = n;
heap->len = 0;
return heap;
}
void swapFun(int *a, int *b) {
*a ^= *b;
*b ^= *a;
*a ^= *b;
}
void heapInsert(BinaryHeap *heap, Element e) {
// 插入: 插入到尾部, 然后上浮
// [i/2, i, 2i, 2i + 1]
if (heap->len == heap->size)
return;
heap->data[++heap->len] = e;
int i = heap->len;
while (i && heap->data[i] < heap->data[i >> 1]) {
swapFun(&heap->data[i], &heap->data[i >> 1]);
i >>= 1;
}
}
Element getHeapTop(BinaryHeap *heap) {
return heap->data[1];
}
void delHeapTop(BinaryHeap *heap) {
// 取堆顶, 与堆尾交换
int j = 1;
swapFun(&heap->data[j], &heap->data[heap->len]);
--heap->len; // 更新长度(保证不会访问到它)
// 进行下沉: 与更小的子结点进行交换 (如果与次小的交换 那不 还是不满足堆?! 笨~)
// 此处主要是要讨论是否有右结点(防止越界才写怎么多if的)
int k = j << 1;
while (k <= heap->len) {
if (k + 1 <= heap->len) {
if (heap->data[k] < heap->data[k + 1]) {
if (heap->data[j] > heap->data[j << 1]) {
swapFun(&heap->data[j], &heap->data[k]);
j <<= 1;
} else
break;
} else {
if (heap->data[j] > heap->data[k + 1]) {
swapFun(&heap->data[j], &heap->data[k + 1]);
j = k + 1;
} else
break;
}
} else {
if (heap->data[j] > heap->data[k]) {
swapFun(&heap->data[j], &heap->data[k]);
j <<= 1;
} else
break;
}
k = j << 1;
}
}
/** 输出
* 1. 将堆顶元素和堆尾元素交换。
* 2. 将堆的大小减一(len--),即排除了已经取出的堆顶元素。
* 3. 对新的堆顶元素进行下沉操作,使其找到正确的位置。
* 4. 重复步骤 1-3,直到堆的大小为 1,即所有元素都已经取出并放入有序的输出序列中。
*/
void heapPrint(BinaryHeap *heap) {
// 拷贝一份用于输出
BinaryHeap *heapCopy = (BinaryHeap *)malloc(sizeof(BinaryHeap));
heapCopy->data = (int *)malloc(sizeof(int) * (heap->len + 1));
for (int i = 1; i <= heap->len; ++i) {
heapCopy->data[i] = heap->data[i];
}
heapCopy->len = heapCopy->size = heap->len;
// 进行输出
for (int i = 1; i <= heapCopy->size; ++i) { // i 只用于计数
printf("%d%c", getHeapTop(heapCopy), i == heapCopy->size ? '\n' : ' ');
delHeapTop(heapCopy);
}
free(heapCopy->data);
free(heapCopy);
}
int main(void) {
// 复习写堆排序
srand(time(NULL));
int n = 17;
int a = 10, b = 100;
BinaryHeap *h = createHeap(n);
for (int i = 0; i < n; ++i)
heapInsert(h, (rand() % (b - a + 1)) + a);
heapPrint(h);
// free堆, 你自己写
getchar();
return 0;
}

