差分数组
例题
张三有如下操作:
- 对 数组的 区间加上 .
- 对 数组的 区间减去 .
输出最终的数组的样子. (会执行 次操作, )
解决
对于区间 加减同一个数的操作 (注意不是赋值), 我们可以使用差分数组, 时间复杂度为:
- 区间加减:
- 区间查询:
而且比普通线段树的代码要轻量级得多! 当然对于特定的题目, 肯定也快得多!
原理
下面是原本是数组arr(即序列A)进行了修改:
- 下标i = [1, 7] 加 2
- 下标i = [2, 5] 加 3
| ##container## |
|---|
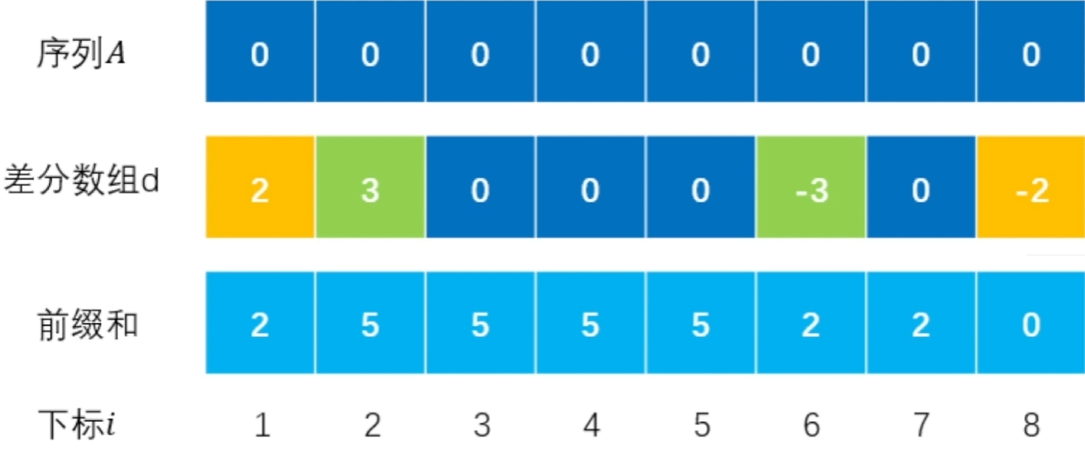 |
可以知道, 对 差分数组 使用一次前缀和就可以还原到修改后的数组! 查询的时间复杂度就是求前缀和的复杂度
以下是模版:
int n;
cin >> n;
vector<int> arr(n);
// 如果arr没有超过int, 那么差分理论上也不会超过int
// n + 1是防止 R + 1 时候的越界, 实际上求和的时候不会用到它
vector<int> dArr(n + 1);
// vector<int> sumArr(n + 1); // 可以没有
// 修改 [L, R] 区间的数 += x
void add(int L, int R, int x) {
dArr[L] += x;
dArr[R + 1] -= x;
}
// 得到最终结果
for (int i = 0, sum = 0; i < n; ++i) {
sum += dArr[i];
cout << i << ": " << arr[i] + sum << '\n';
}
练习
有时候需要按照题目要求区分边界, 不一定题目是修改 , 有时候会是 等哦~

