图的存储
图在内存中存储方式有很多种,最经典的包括邻接矩阵、邻接表、逆邻接表和十字链表。
图的存储结构相比较线性表与树来说就复杂很多。
回顾一下上面提到的,对于线性表来说,是一对一的关系,所以用数组或者链表均可简单存放。树结构是一对多的关系,所以我们要将数组和链表的特性结合在一起才能更好的存放。
那么图,是多对多的情况,图上的任何一个顶点都可以被看作是第一个顶点,任一顶点的邻接点之间也不存在次序关系。
因为任意两个顶点之间都可能存在联系,因此无法以数据元素在内存中的物理位置来表示元素之间的关系(内存物理位置是线性的,图的元素关系是平面的)。
如果用多重链表来描述倒是可以做到,但是纯粹用多重链表导致的浪费是无法想像的(如果各个顶点的度数相差太大,就会造成巨大的浪费)。
邻接矩阵
图的邻接矩阵是用两个数组来表示,一个一维数组存储图中的顶点信息,一个二维数组(我们将这个数组称之为邻接矩阵)存储图中的边的信息。
无向图邻接矩阵
我们可以设置两个数组,顶点数组为vertex[4]={V0,V1,V2,V3},边数组arc[4][4]为对称矩阵(0表示不存在顶点间的边,1表示顶点间存在边)。
对称矩阵
所谓对称矩阵就是n阶矩阵的元素满足 。即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的。
| ##container## |
|---|
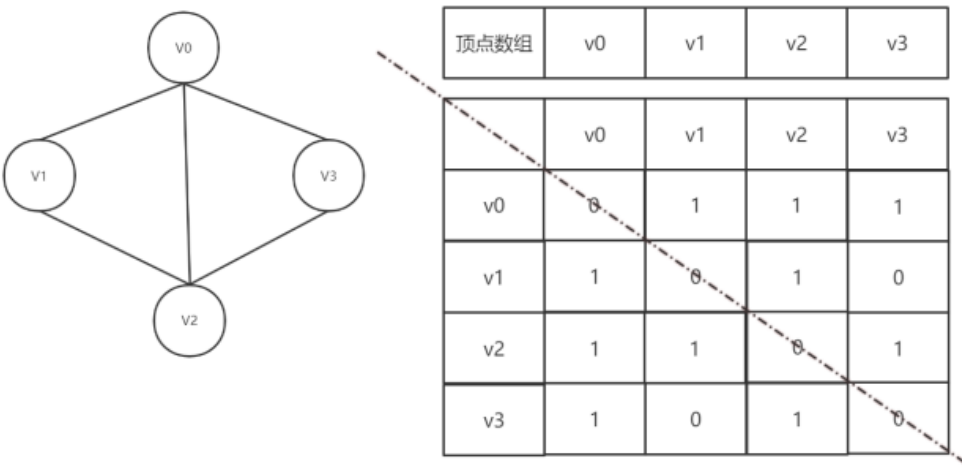 |
有了这个二维数组组成的对称矩阵,我们就可以很容易地知道图中的信息:
- 判定任意两顶点是否有边无边;
- 可以轻松知道某个顶点的度,其实就是这个顶点Vi在邻接矩阵中第i行(或第i列)的元素之和;
- 求顶点Vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点喽。
有向图邻接矩阵
无向图的边构成了一个对称矩阵,貌似浪费了一半的空间,那如果是有向图来存放,会不会把资源都利用得很好呢?
| ##container## |
|---|
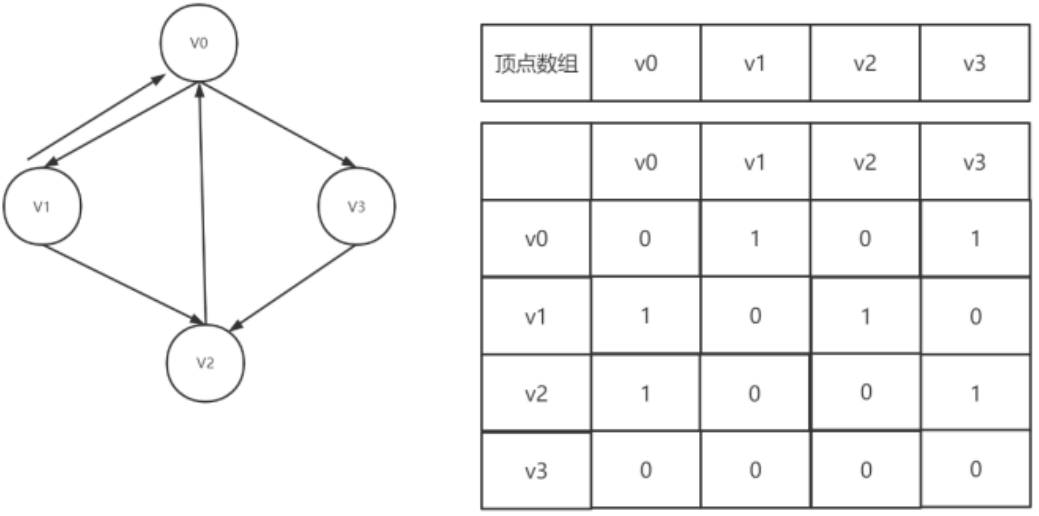 |
可见顶点数组vertex[4]={V0,V1,V2,V3},弧数组arc[4][4]也是一个矩阵,但因为是有向图,所以这个矩阵并不对称,例如由V0到V3有弧,得到arc[0][3]=1,而V3到v0没有弧,因此arc[3][0]=0。
另外有向图是有讲究的,要考虑入度和出度,顶点V1的入度为1,正好是第V1列的各数之和,顶点V1的出度为2,正好是第V1行的各数之和。
带权图的邻接矩阵
带权图中的每一条边上带有权值,邻接矩阵中的值则为权值,当两个顶点之间没有弧时,则用无穷大表示。
| ##container## |
|---|
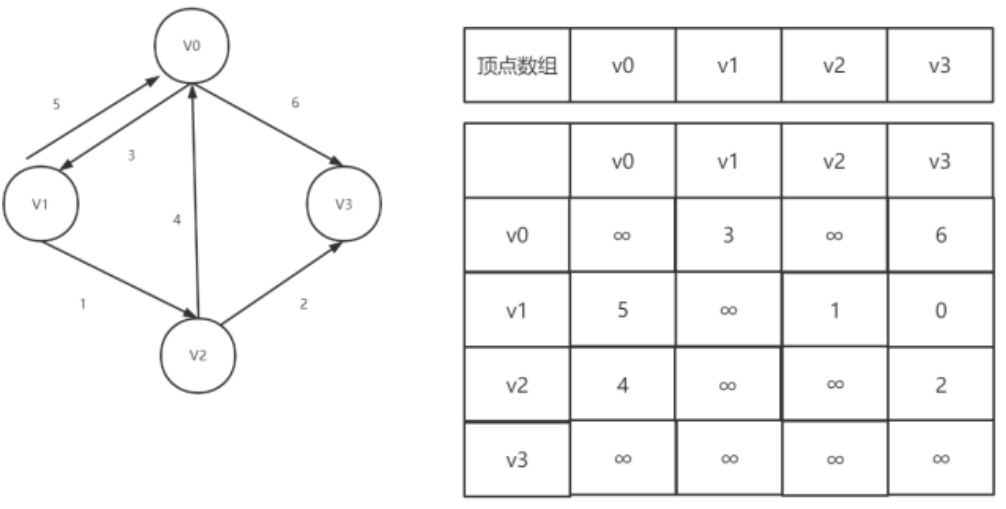 |
这里“∞”表示一个计算机允许的、大于所有边上权值的值。
这个时候我们会发现一个问题,就是空间浪费问题。尤其是面对边数相对比较少的稀疏图来说,这种结构无疑是存在对存储空间的极大浪费。
因此我们可以考虑另外一种存储结构方式,例如把数组与链表结合在一起来存储,这种方式在图结构也适用,我们称为邻接表(Adjacency List)。
邻接表
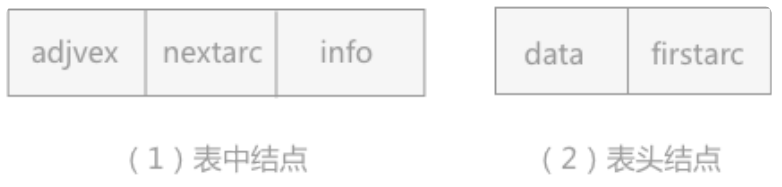
邻接表的处理方法是这样:
-
图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过数组可以较容易地读取顶点信息,更加方便。
-
图中每个顶点 的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以我们选择用单链表来存储。
| ##container## |
|---|
 |
无向图邻接表
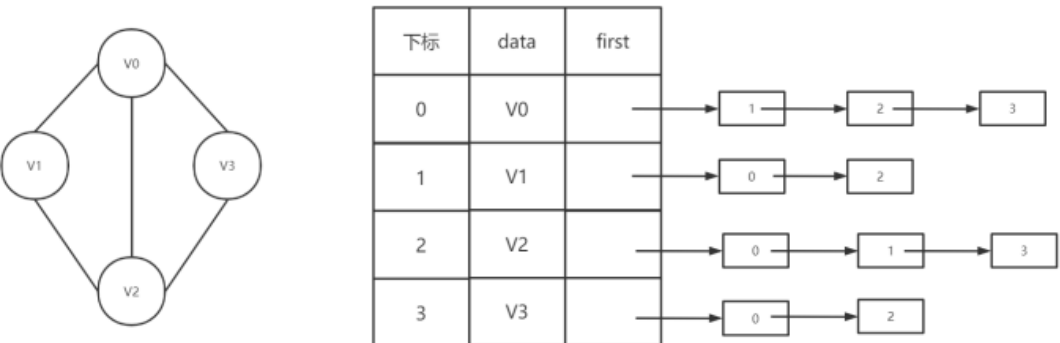
有向图邻接表
若是有向图,邻接表结构也是类似的,我们先来看下把顶点当弧尾建立的邻接表,这样很容易就可以得到每个顶点的出度:
| ##container## |
|---|
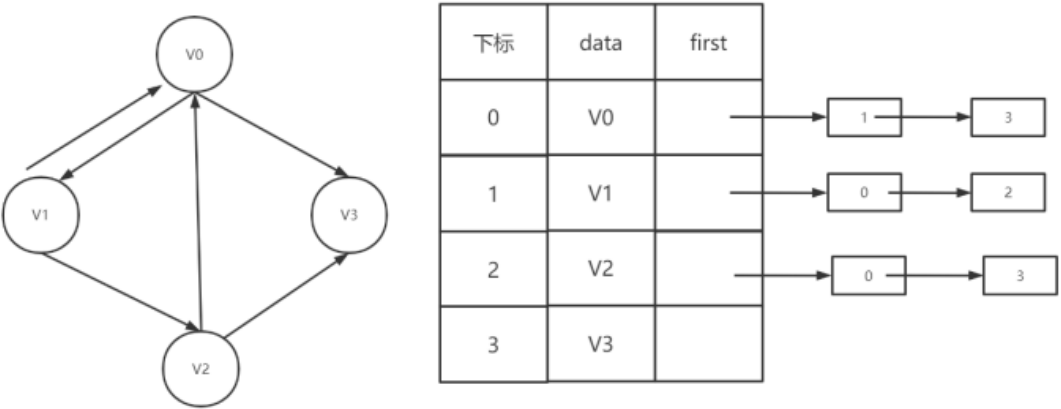 |
但也有时为了便于确定顶点的入度或以顶点为弧头的弧,我们可以建立一个有向图的逆邻接表:
| ##container## |
|---|
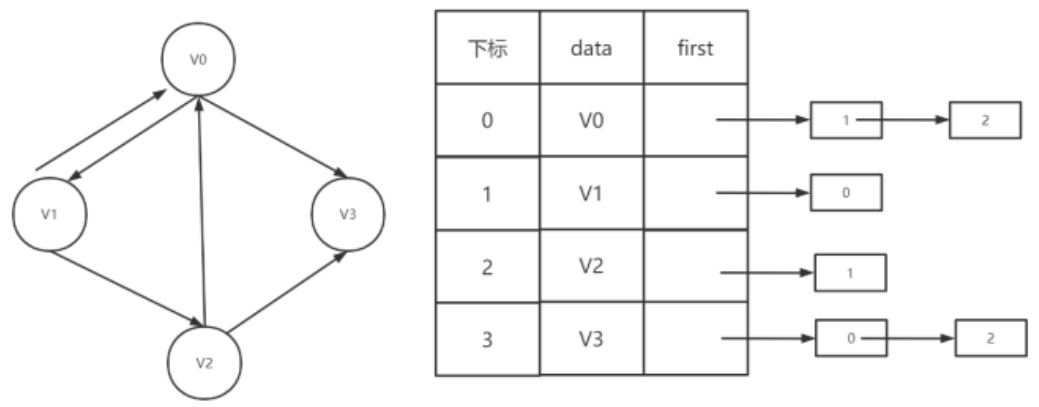 |
带权网络的邻接表
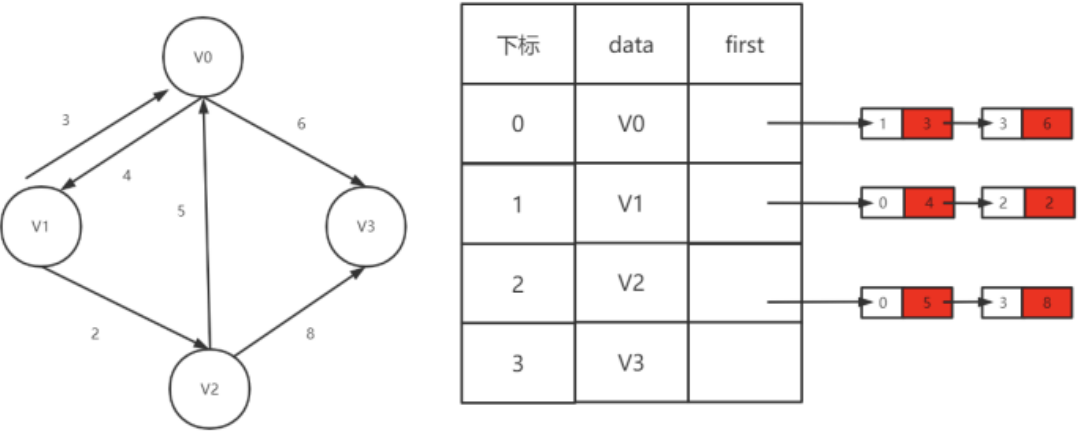
邻接表固然优秀,但也有不足,例如对有向图的处理上,有时候需要再建立一个逆邻接表~
这个时候,我们可以想一下,我们是否可以把邻接表和逆邻接表结合起来呢?
当然可以,这个就是十字链表。
十字链表表示
十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以Vi为尾的弧,也容易找到以 为头的弧,因而容易求得顶点的出度和入度。
十字链表除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的,因此,在有向图的应用中,十字链表也是非常好的数据结构模型。
| ##container## | |:--:| |数据结构| |
| |
| |实例| |
|
这个时候,还有一个问题,如果使用邻接表存储结构,但是对边的操作比较频繁,怎么办?
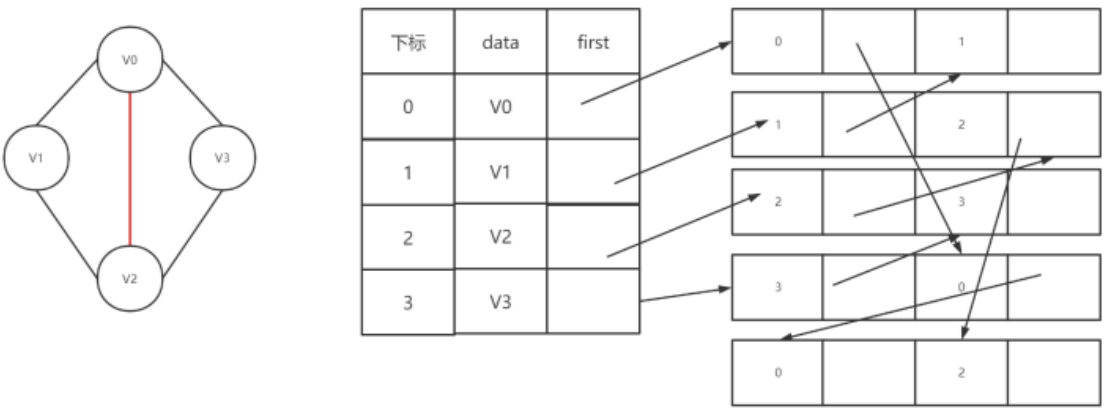
如果我们在无向图的应用中,关注的重点是顶点的话,那么邻接表是不错的选择,但如果我们更关注的是边的操作,比如对已经访问过的边做标记,或者删除某一条边等操作,邻接表的确显得不那么方便了(下图中删除红色边)。
邻接多重表
邻接表对边的操作显然很不方便,因此,我们可以仿照十字链表的方式,对边表结构进行改装,重新定义的边表结构如下:
| ##container## |
|---|
 |
其中iVex和jVex是与某条边依附的两个顶点在顶点表中的下标。
iLink指向依附顶点iVex的下一条边,jLink指向依附顶点jVex的下一条边。
| ##container## |
|---|
 |
边集数组
边集数组是由两个一维数组构成,一个是存储顶点的信息,另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。
| ##container## |
|---|
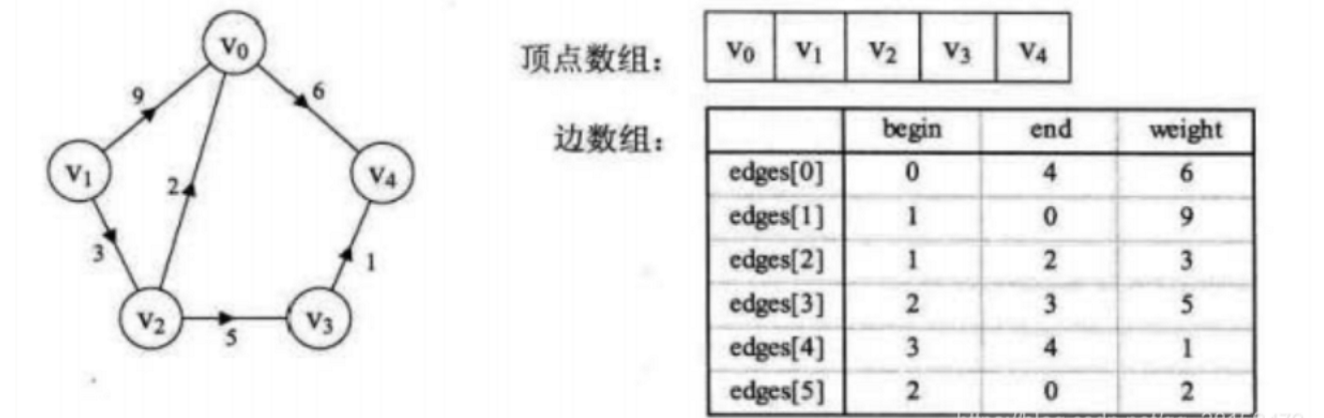 |
| 性质:如上图所示,边集数组关注的是边的集合,在边集数组中要查找一个顶点的度需要扫描整个边数组,效率并不高。 |
因此它更适合对边依次进行处理的操作,而不适合对顶点相关的操作。
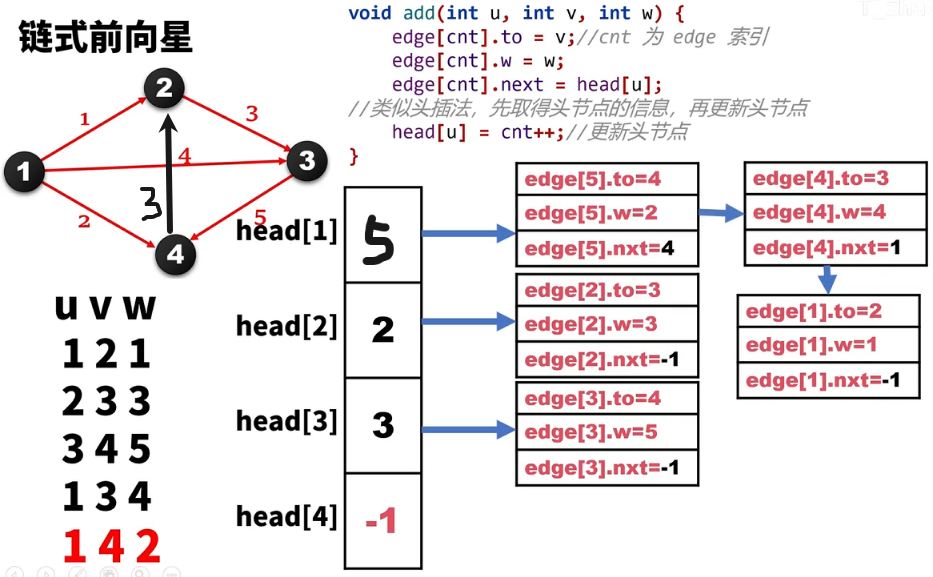
链式前向星
因为邻接表写得很麻烦, 但邻接矩阵又占用了 的空间复杂度, 对于 的图, 一般是会爆内存的.
因此有了这个「链式前向星」的数据结构, 相当于 邻接表的静态链表的表示 (因为一般不会涉及删除(因为是竞赛中使用))
#define MAX ((int)1e5 + 1)
typedef struct _edge
{
int to; // 连接的点
int next; // 下一个边
int w; // 权值
} Edge;
int n; // 节点个数
Edge edge[MAX]; // edge[i] 存储第i条边的信息
int head[MAX]; // head[i] 存储以i为起点的所有边的起始位置
int edge_cnt = 1; // edge_cnt 为 edge 的索引
void add_edge(int u, int v, int w)
{ // u --w--> v
edge[edge_cnt].to = v;
edge[edge_cnt].w = w;
edge[edge_cnt].next = head[u];
head[u] = edge_cnt++;
}
void print_edge(void)
{
for (int i = 1; i <= n; ++i)
for (int j = head[i]; j != 0; j = edge[j].next)
printf("%d --%d--> %d\n", i, edge[j].w, edge[j].to);
}
| ##container## |
|---|
 |

