计数排序

前面介绍的冒泡，选择，插入，归并，快速，希尔，堆排序，都是基于比较的排序，这些基于比较的排序，有以下几个特点：平均时间复杂度最低的是 $O(nlogn)$
而计数排序，不是基于比较的排序。其中不基于比较的排序还有桶排序，基数排序等
它们是典型的用空间换时间，在某些时候，平均时间复杂度可以比 $O(nlogn)$ 更低，也就是说，在某些时候，这种利用空间换时间的排序算法，性能比前面基于比较的排序算法更快。

概述

计数排序是在1954年由HaroldH.Seward提出，适合对一定范围内的整数进行排序。计数排序核心思想

统计每个整数在序列中出现的次数，进而推导出每个整数在有序序列中的索引。

我们以数组[1,4,1,2,5,2,4,1,8]为例进行说明。
第一步：建立一个初始化为0，长度为9（原始数组中的最大值8 加 1）的数组count[]。
第二步：遍历数组[1,4,1,2,5,2,4,1,8]，访问第一个元素 1，然后将数组下标为 1的元素加 1，表示当前 1 出现了一次，即 count[1] = 1;

依次遍历，对count进行统计。

伪代码: 类似于数组下标实现的哈希表

void 计数排序(vector<int>& arr) {
    int lenMax = 0;
    for (auto& it : arr)
        lenMax = max(it, lenMax);

    // 进行计数
    vector<int> count(lenMax, 0);
    for (auto& it : arr)
        ++count[it];

    // 输出
    for (int i = 0; i < lenMax; ++i)
        for (int j = 0; j < count[i]; ++j)
                printf("%d ", i);
}
C++

计数排序的改进

上述算法的问题如下：

无法对负整数进行排序
极其浪费内存空间
是一个不稳定排序

改进一

只要不再以输入数列的[最大值+1]，作为统计数组的长度，而是以数列[最大值-最小值+1]作为统计数组的长度即可。数列的最小值作为一个偏移量，用于计算整数在统计数组中的下标。

比如，假设下面的数组的数列：
95,94, 91, 98, 99,90, 99, 93,91, 92

统计出数组的长度为 $99-90+1=10$ ,偏移量等于数列的最小值 $90$ 。对于第1个整数 $95$ ，对应的统计数组下标是 $95-90=5$ 。

改进二

不用看这里

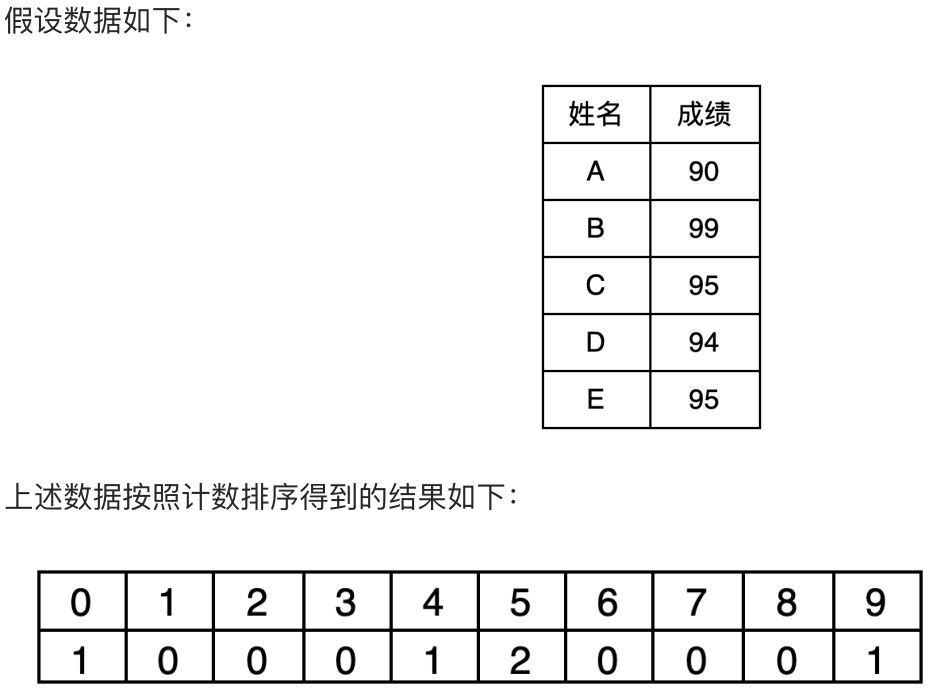
Clip_2024-02-16_10-43-12.png ##w600##

如何判断5中的2个人谁是C谁是E呢? 那么需要进行变形。

这是如何变形的呢？其实就是从统计数组的第2个元素开始，每一个元素都加上前面所有元素之和。

这样相加的目的，是让统计数组存储的元素值，等于相应整数的最终排序位置的序号。例如，下标是9的元素值为5，代表原始数列的整数9，最终的排序在第5位。

Clip_2024-02-16_10-45-07.png ##w600##

首先，遍历成绩表最后一行E的成绩，E是95，那么5下标元素是4，表示E在最后的排名在第4位，同时将原来的值减1，表示下次再遇到95的成绩时，最终排名是第3。

~~(还是不理解)~~

桶排序

~~好像是为了解决上面不能解决小数排序的问题?~~

其实桶排序重要的是它的思想，而不是具体实现，桶排序从字面的意思上看：

若干个桶，说明此类排序将数据放入若干个桶中。
每个桶有容量，桶是有一定容积的容器，所以每个桶中可能有多个元素。
从整体来看，整个排序更希望桶能够更匀称，即既不溢出(太多)又不太少假设有一个非整数数列，如下：
4.5, 0.84, 3.25, 2.18, 0.5
桶排序的第1步，就是创建这些桶，并确定每一个桶的区间范围。

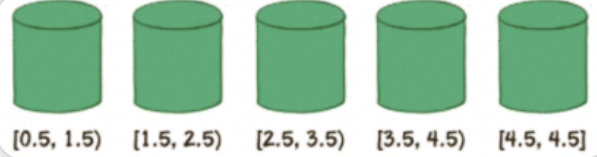
Clip_2024-02-16_10-53-37.png ##w400##