什么是最小生成树
生成树的定义
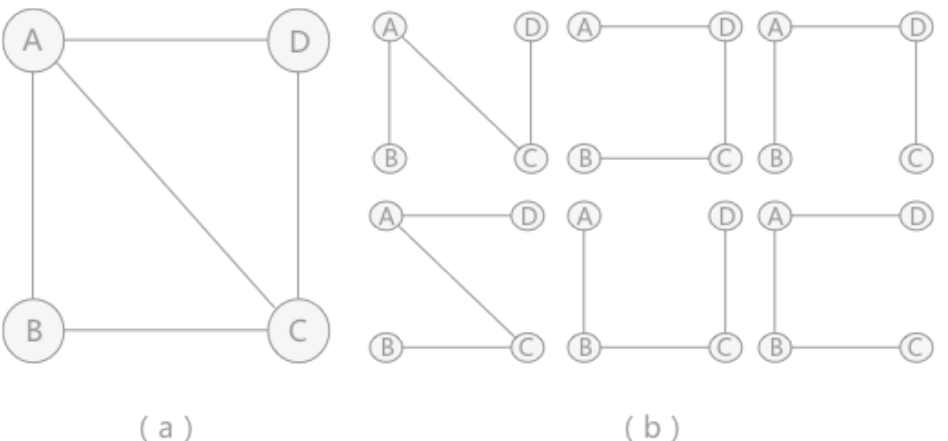
一个连通图的生成树是一个极小的连通子图,它包含图中全部的n个顶点,但只有构成一棵树的n-1条边。
| ##container## |
|---|
 |
实际作用
连通图和它相对应的生成树,可以用于解决实际生活中的问题:假设A、B、C 和 D为 4 座城市,为了方便生产生活,要为这4 座城市建立通信。对于4个城市来讲,本着节约经费的原则,只需要建立3个通信线路即可,就如图(b)中的任意一种方式。
在具体选择采用(b)中哪一种方式时,需要综合考虑城市之间间隔的距离,建设通信线路的难度等各种因素,将这些因素综合起来用一个数值表示,当作这条线路的权值。
| ##container## |
|---|
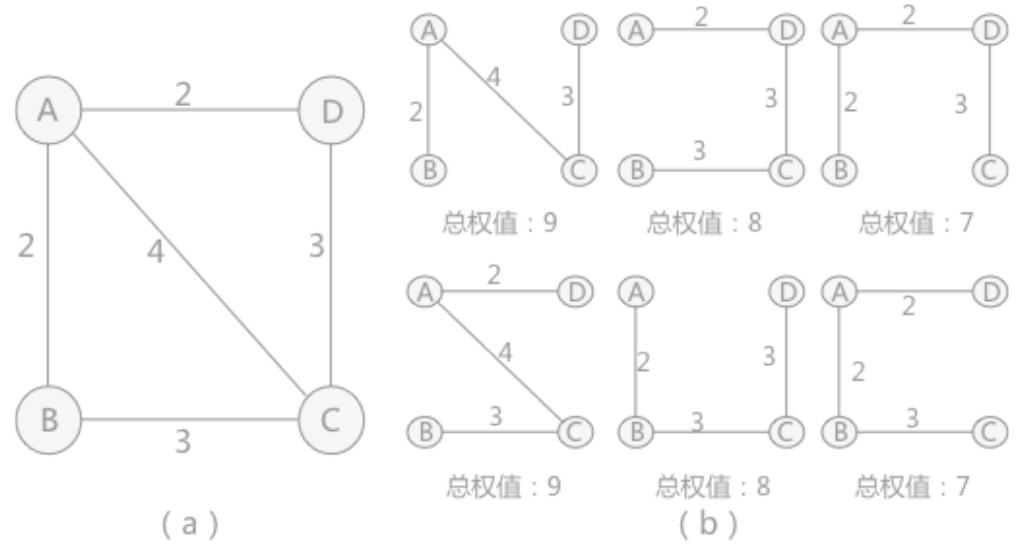 |
综合所看,选择权值总和为7的两种方案最节约经费。
生成树的属性
- 一个连通图可以有多个生成树;
- 一个连通图的所有生成树都包含相同的顶点个数和边数;
- 生成树当中不存在环;
- 移除生成树中的任意一条边都会导致图的不连通,生成树的边最少特性;
- 在生成树中添加一条边会构成环。对于包含n个顶点的连通图,生成树包含n个顶点和n-1条边;
- 对于包含 个顶点的无向完全图最多包含 颗生成树。
最小生成树
所谓一个 带权图 的最小生成树,就是原图中边的权值最小的生成树,所谓最小是指边的权值之 和小于或者等于其它生成树的边的权值之和。
最小生成树的算法思想就是从顶点集或边集的角度来进行贪婪化。
相关算法
总结
最小生成树的问题,简单得理解就是给定一个带有权值的连通图(连通网),从众多的生成树中筛选出权值总和最小的生成树,即为该图的最小生成树。
最经典的两个最小生成树算法:Kruskal算法与Prim算法。两者分别从不同的角度构造最小生成树,Kruskal算法从边的角度出发,使用贪心的方式选择出图中的最小生成树,而Prim算法从顶点的角度出发,逐步找各个顶点上最小权值的边来构建最小生成树的。
最小生成树问题应用广泛,最直接的应用就是网线架设(网络G表示n各城市之间的通信线路网线路(其中顶点表示城市,边表示两个城市之间的通信线路,边上的权值表示线路的长度或造价。可通过 求该网络的最小生成树达到求解通信线路或总代价最小的最佳方案。或者如果我们需要用最少的电线给所房子安装电路。)、道路铺设。还可以间接应用于纠错的LDPC码、Renyi 熵图像配准、学习用于实时脸部验证的显著特征、减少蛋白质氨基酸序列测序中的数据存储,在湍流(turbulent)中模拟粒子交互的局部性,以及用于以太网桥接的自动配置,以避免在网络中形成环路。除此之外,最小生成树在聚类算法中也是应用广泛。

