图的遍历
深度优先遍历 (DFS)
简称深搜或DFS
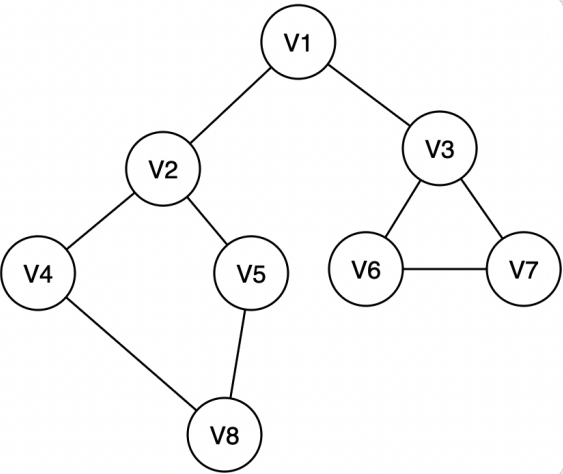
深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。例如上图是一个无向图,采用深度优先算法遍历这个图的过程为:
-
首先任意找一个未被遍历过的顶点,例如从V1开始,由于V1率先访问过了,所以,需要标记V1的状态为访问过;
-
然后遍历V1的邻接点,例如访问V2,并做标记,然后访问V2的邻接点,例如V4(做标记),然后V8,然后V5;
-
当继续遍历V5的邻接点时,根据之前做的标记显示,所有邻接点都被访问过了。此时,从V5回退到V8,看V8 是否有未被访问过的邻接点,如果没有,继续回退到V4,V2,V1;
-
通过查看V1,找到一个未被访问过的顶点V3,继续遍历,然后访问V3邻接点V6,然后V7;
-
由于V7没有未被访问的邻接点,所有回退到V6,继续回退至V3,最后到达V1,发现没有未被访问的;
-
最后一步需要判断是否所有顶点都被访问,如果还有没被访问的,以未被访问的顶点为第一个顶点,继续依照上边的方式进行遍历。
根据上边的过程,可以得到上图通过深度优先搜索获得的顶点的遍历次序为:
V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7
所谓深度优先搜索,是从图中的一个顶点出发,每次遍历当前访问顶点的临界点,一直到访问的顶点没有未被访问过的临界点为止。
然后采用依次回退的方式,查看来的路上每一个顶点是否有其它未被访问的临界点。访问完成后,判断图中的顶点是否已经全部遍历完成,如果没有,以未访问的顶点为起始点,重复上述过程。
深度优先搜索是一个不断回溯的过程。
通常的, dfs需要用到栈, 代码上可以通过递归实现.
广度优先搜索
广度优先搜索类似于树的层次遍历。从图中的某一顶点出发,遍历每一个顶点时,依次遍历其所有的邻接点,然后再从这些邻接点出发,同样依次访问它们的邻接点。按照此过程,直到图中所有被访问过的顶点的邻接点都被访问到。
最后还需要做的操作就是查看图中是否存在尚未被访问的顶点,若有,则以该顶点为起始点,重复上述遍历的过程。
还拿上图的无向图为例,假设V1作为起始点,遍历其所有的邻接点V2 和V3,以V2为起始点,访问邻接点V4 和V5,以V3为起始点,访问邻接点V6、V7,以V4为起始点访问V8,以V5为起始点,由于V5 所有的起始点已经全部被访问,所有直接略过,V6 和V7也是如此。
以V1为起始点的遍历过程结束后,判断图中是否还有未被访问的点,由于图1中没有了,所以整个图遍历结束。遍历顶点的顺序为:
V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> v8
通常的, bfs需要用到队列, 代码需要显式的使用一个队列.
代码
请见: 图的存储and遍历code

