子集型回溯
学习视频: 回溯算法套路①子集型回溯【基础算法精讲 14】
课上题目 + 多语言代码:
- 17. 电话号码的字母组合
- 78. 子集
- 131. 分割回文串 (包含一种判断回文字符串的方法 双指针)
课后作业:
- 784. 字母大小写全排列
- LCP 51. 烹饪料理
- 2397. 被列覆盖的最多行数
- 2151. 基于陈述统计最多好人数
- 1601. 最多可达成的换楼请求数目
- 306. 累加数
- 93. 复原 IP 地址
- 2698. 求一个整数的惩罚数
递归 , 那么就不会出错, 剩下的交给数学归纳法就OK
| ##container## |
|---|
   |
组合型回溯
组合型回溯, 相当于在
子集型回溯里面增添了一个剪枝操作.
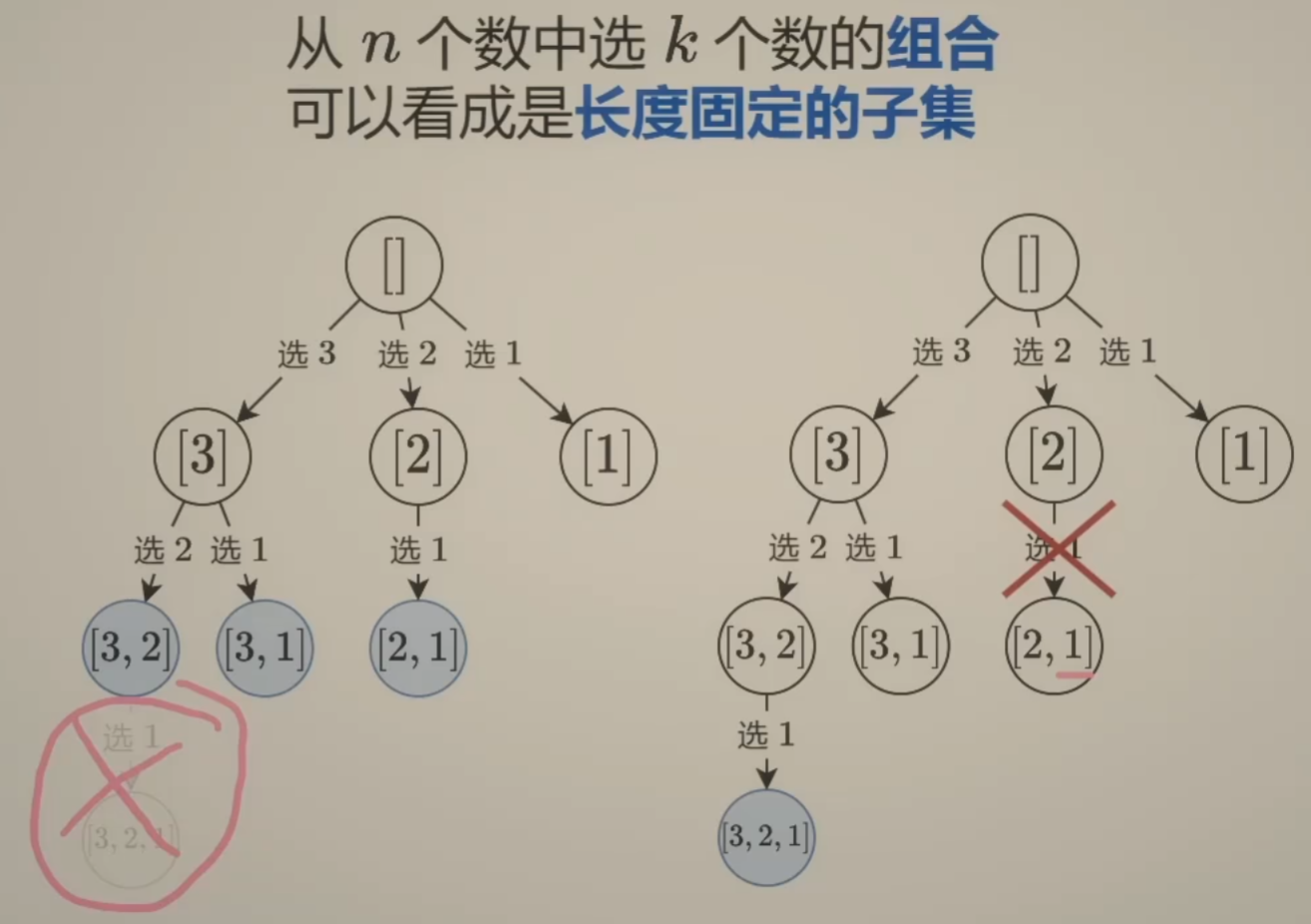
例如: 77. 组合
给定两个整数n和k,返回范围[1, n]中所有可能的k个数的组合。
你可以按 任何顺序 返回答案。
示例:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2], // [1, 2] 和 [2, 1] 是同一种答案
[1,3],
[1,4],
]
- 注: 此处的组合和子集, 就类似于 与 的关系一样
| ##container## |
|---|
  |
代码:
方法一:枚举下一个数选哪个 (枚举即有for)
class Solution {
public:
vector<vector<int>> combine(int n, int k) {
vector<vector<int>> res;
vector<int> arr;
function<void(int, int)> dfs =
[&](int i, int len) {
if (len == k) {
res.push_back(arr);
return;
}
if (i - k >= n)
return;
// 枚举
for (int index = i; index < n; ++index) {
arr.push_back(index + 1);
dfs(index + 1, len + 1);
arr.pop_back();
}
};
dfs(0, 0);
return res;
}
};
方法二:选或不选
class Solution {
public:
vector<vector<int>> combine(int n, int k) {
/*
选或者不选, ~~需要记录是否选择了~~ <--无需!
*/
vector<vector<int>> res;
vector<int> arr;
function<void(int, int)> dfs =
[&](int i, int len) {
if (i - k >= n
|| i > n)
return;
if (len == k) {
res.push_back(arr);
return;
}
// 不选
dfs(i + 1, len);
// 选
arr.push_back(i + 1);
dfs(i + 1, len + 1);
arr.pop_back();
};
dfs(0, 0);
return res;
}
};
学习视频: 回溯算法套路②组合型回溯+剪枝【基础算法精讲 15】
课后作业:
课后作业: 换一种写法完成上面三题。

