单调栈

学习链接: 单调栈【基础算法精讲 26】

例题一: 739. 每日温度

给定一个整数数组temperatures，表示每天的温度，返回一个数组answer，其中answer[i]是指对于第i天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用0来代替。

有两种思考方式:

从右到左

##container##

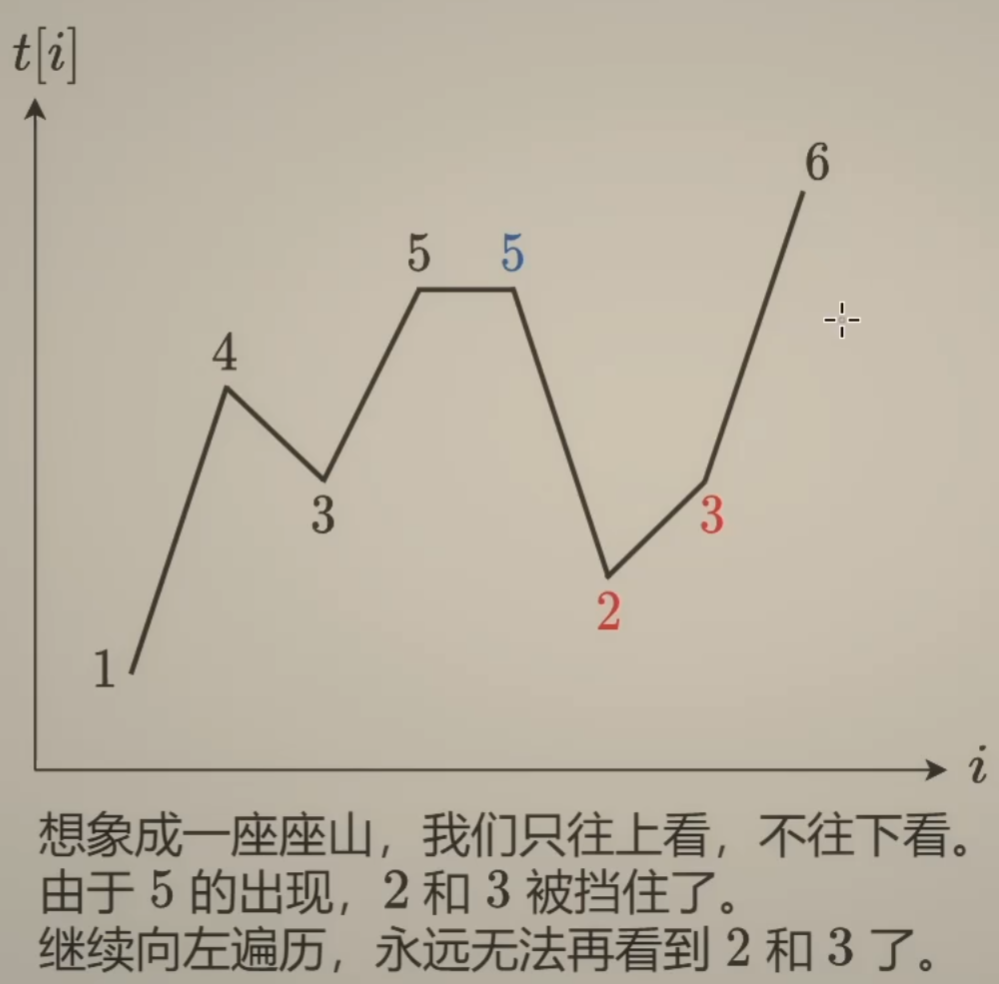比如我们从 6 -> 3 -> 2 -> 5, 此时在5处往右看, 就只能看见 比5大的6 了, 而看不见 2, 3;

当我们继续走: 5 -> 5 -> 3 -> 4, 此时在4处往右看, 就只能看见 比4大的5(或者6) 了, 而看不见 3;

由上可见, 因为往后看只能看到比自己高的, 因此具有单调性, 当一个新的数据到来, 发现比当前的栈顶高, 那么栈顶元素就变成垃圾数据了, 因为站到新数据的位置, 看不到栈顶(比它低的), 而再后来的也看不到比它低的, 因为已经被这个新数据"挡住"了.

代码如下:

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        vector<int> res(n);
        stack<int> S; // 索引
        for (int i = n - 1; i >= 0; --i) {
            while (S.size() && temperatures[i] >= temperatures[S.top()]) {    
                S.pop();
            }
            
            if (S.size())
                res[i] = S.top() - i;

            S.push(i);
        }

        return res;
    }
};

C++

从左到右

这个方向的思路才更符合单调栈的思考(0x3f)

我们把"从右到左"反过来, 不就得到了"从左到右"的方案了吗?

把当前元素入栈, 如果后面的元素比栈顶高, 那么栈顶出栈, 并且更新answer(说明已经找到比栈顶元素高的元素), 一直判断出栈, 直到不符合, 再把后面的元素入栈, 表示要找比后面元素高的点

代码如下:

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        vector<int> res(n);
        stack<tuple<int, int>> S; // 温度 - 索引
        S.push({101, -1}); // 小技巧, 这样可以不用判断栈是否为空

        for (int i = 0; i < n; ++i) {
            auto [w, index] = S.top();
            while (w < temperatures[i]) {
                res[index] = i - index;
                S.pop();
                tie(w, index) = S.top();
            }
            S.push({temperatures[i], i});
        }

        return res;
    }
};

C++

当然可以简化一下, 栈里面直接存放索引即可:

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        vector<int> res(n);
        stack<int> S; // 索引

        for (int i = 0; i < n; ++i) {
            while (S.size() && temperatures[S.top()] < temperatures[i]) {
                res[S.top()] = i - S.top();
                S.pop();
            }
            S.push(i);
        }

        return res;
    }
};

C++

例题二: 42. 接雨水

给定n个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

##container##
初始
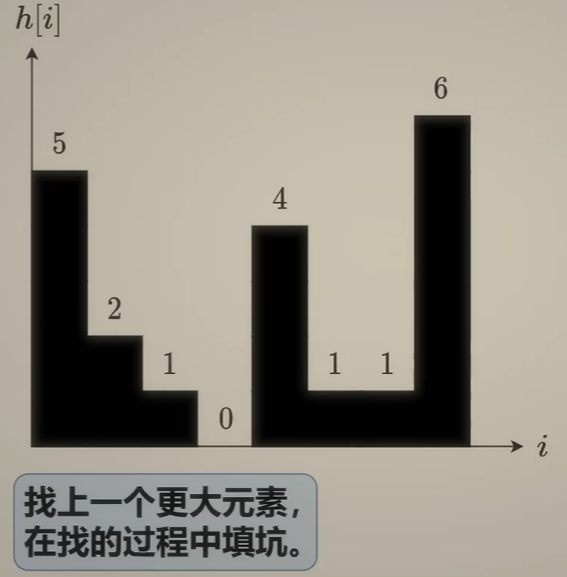遇到比左边大的, 比如4, 此时可以往右边找比它小的
比如1, 1和4的公共高度(短板)是 $min(1, 4)=1$,
而宽度是[4的索引减1的索引 - 1]
故可以装水 $S_{_水}=h*L=1*1=1$
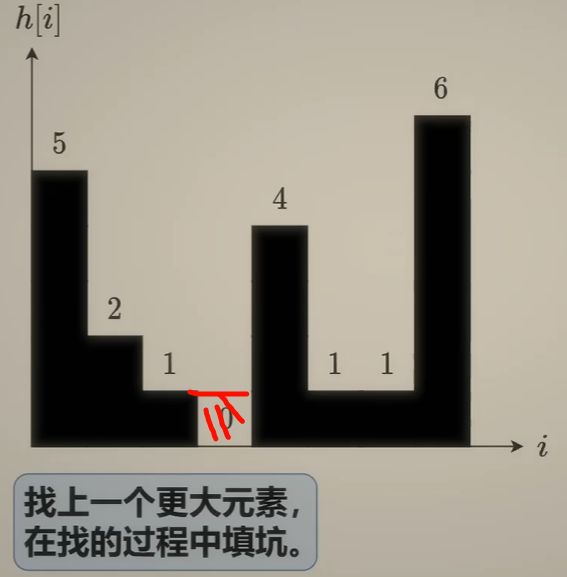继续循环判断, 直到左边没有比4小的
(现在装水为蓝色部分, 可以视作之前装的是水泥, 把坑填上了(不会重复计算))
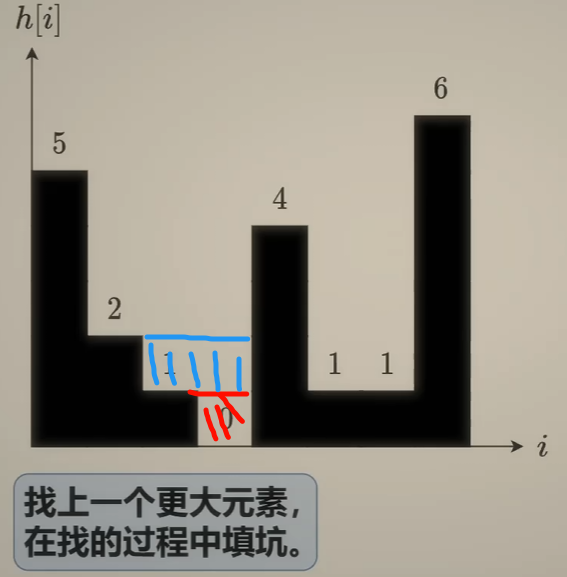同理

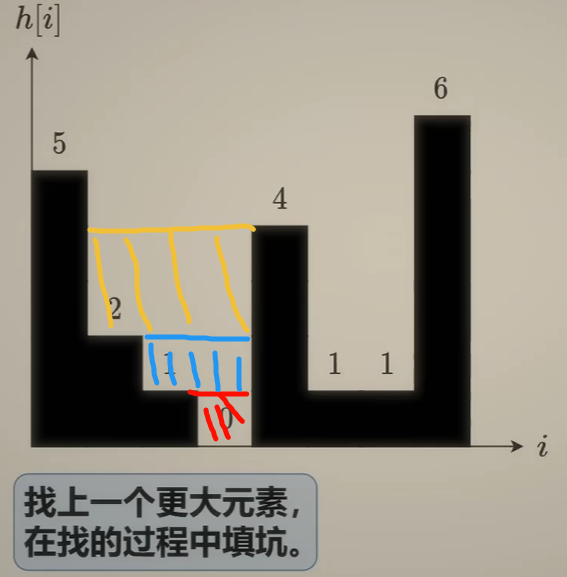代码: (可以发现上面需要三个变量 右边的边4, 底部的高度, 左边的边(比底部边高)(即 栈需要长度为2才有作为))

class Solution {
public:
    int trap(vector<int>& height) {
        int res = 0;
        stack<int> S; // 索引
        S.push(0);
        for (int i = 1; i < height.size(); ++i) {
            int index = S.top();
            while (height[index] < height[i]) {
                S.pop();
                if (!S.size())
                    break;
                int mototakai = S.top();
                res += (i - mototakai - 1) * (min(height[mototakai], height[i]) - height[index]);
                index = mototakai;
            }
            S.push(i);
        }
        return res;
    }
};

C++

何时 使用/需要思考到 单调栈

如果你发现要计算的内容涉及到上一个或者下一个更大或更小元素, 可以尝试使用单调栈解决.

• 子数组+单调性-->要想到单调栈(这是一个套路) (但不是只有子数组才可以用单调栈, 有这种性质需求的子序列也不是不行(1673. 找出最具竞争力的子序列))
• 或者说, 我存在这种性质: 我可以用我当前遍历过的数, 去把之前遍历的数据判断成垃圾数据. 这样的题目就可以使用单调栈来做^[1]

相关题目

• 3113. 边界元素是最大值的子数组数目 (128场双周赛Q4)

• 思考题

  • 改成子数组第一个 或 最后一个元素是最大值，要怎么做？
  • 改成子数组第一个元素是最大值，最后一个元素是 最小值，要怎么做？
  • 改成树上路径问题，见 [2421. 好路径的数目]。本题相当于把 2421 的树特化成一条链。

注解

[1]

来源: Dijkstra 最短路 单调栈【力扣双周赛 128】20:00附近