构建一个基本算数逻辑单元
前言
算术逻辑单元(ALU) 是计算机的核心,ALU 用来执行算术运算,比如加法和减法,也可以用来执行逻辑运算,比如与操作、或操作。
我们将借助 4 个硬件块 (与门、或门、反向器和多路选择器) 来构造一个 ALU, 并演示组合逻辑是如何工作的。
1位 ALU
我们先从简单的 1 bit の ALU 始まり
逻辑单元: 与/或
| ##container## |
|---|
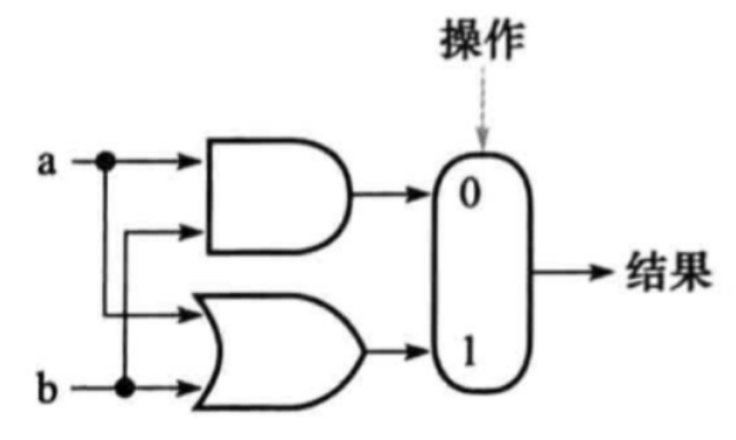 |
Tip
很简单对吧~ 一目瞭然
算术单元: 加法
| ##container## |
|---|
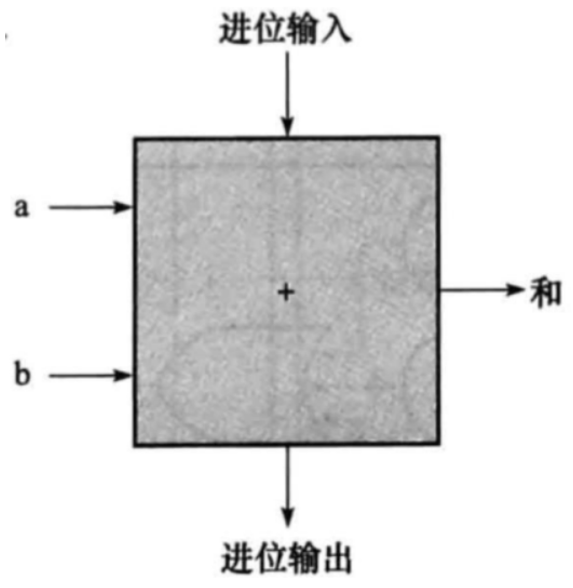 |
进位信号在加法运算中非常重要,当两个数相加的结果超过一位数的表示范围时,就需要用到进位。这个进位信号会传递给下一个加法器或逻辑门,以便进行更高位的加法运算,这个主要是进位输出做的事情。
进位输入信号用于传递上一位加法产生的进位到当前位的加法操作中。这样,即使在处理多个二进制位的加法过程中发生 连续的进位,也能得到正确的结果。
最终,我们将选择控制器和加法器组装在一起,形成了一个1位的ALU。
| ##container## |
|---|
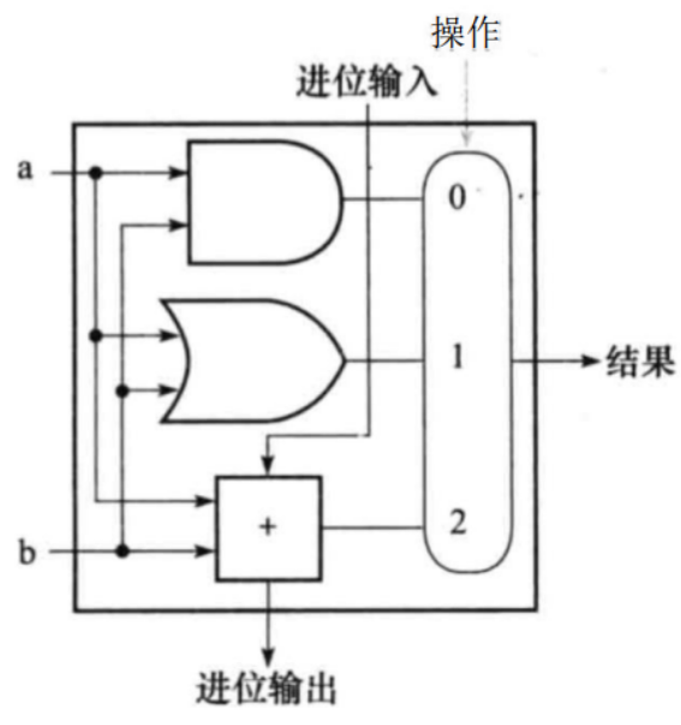 |
加法器的内部硬件构成 (补充,不重要)
| A | B | Sum | Cout |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 |
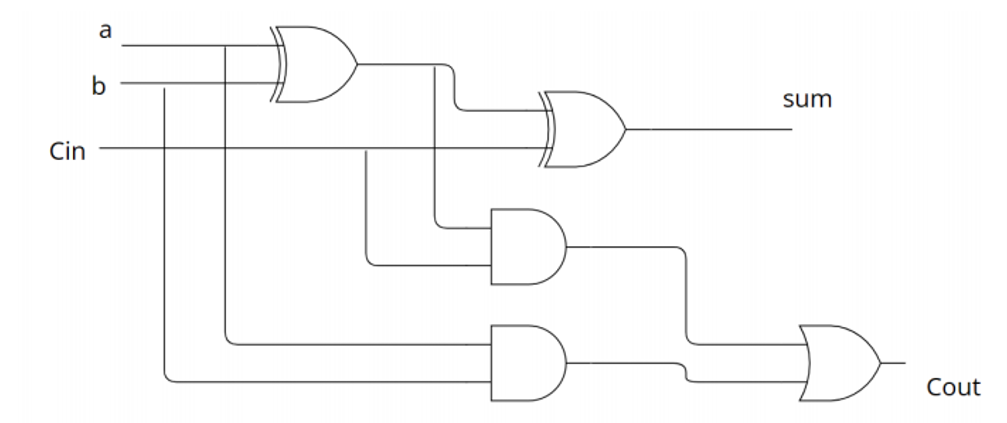
先不考虑低位的进位,不难发现, Sum可以看作由 A 和 B 经过异或运算得到, 而向下一位的进位Cout则是由A 和 B经过与运算得到. 我们用门电路画出来, 就得到了一个半加器。
加法器的内部硬件构成:
| ##container## |
|---|
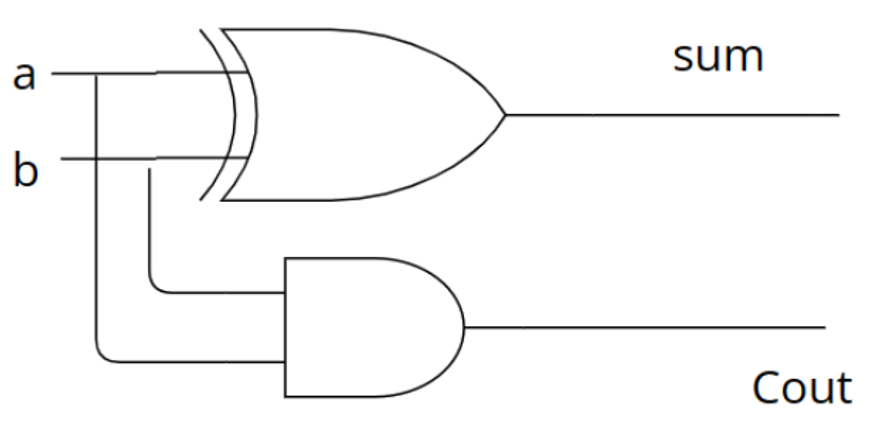 |
接下来, 就是在半加器的基础上让它能处理低位过来的进位。
只需要把刚才半加器得到的和再和进位相加, 就能得到真正的和。
因为我们知道异或可以得到和, 与可以得到进位, 所以在半加器的基础上再添加一个半加器的结构,我们的加法器就变成了能处理进位的全加器。
| A | B | Cin | Sum | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
即:
| ##container## |
|---|
 |
32 位ALU
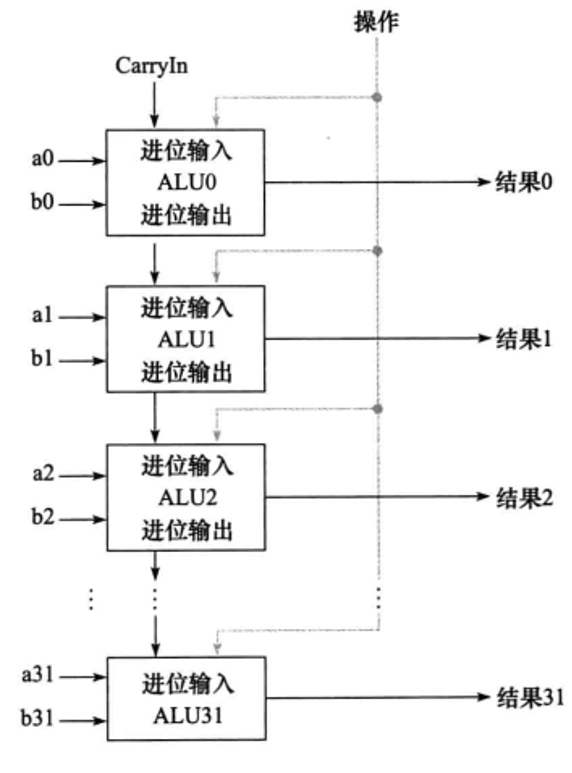
多位的ALU就是用一位ALU组装起来的。我们通过一种特殊的组织方式将其组装起来,这个组织方式叫做 。
行波进位的基本思想是将进位计算分解为两个阶段:
-
进位产生(Generate, G): 判断本位是否直接产生进位,即本位两个输入数据相加是否溢出(即都为1)。
-
进位传递(Propagate, P): 判断本位是否有能力将前一位传来的进位向下一位传递,即本位至少有一个输入数据为1。
每个 1 位 ALU 负责执行基本的算术和逻辑运算,并且在这个结构中,每个 1 位ALU的进位输出作为下一位1位ALU的进位输入,这样逐级连接,形成了“行波”般的进位传播链。同时,通过上述的G和P信号,以及相应的逻辑门网络,可以在每一级快速计算出下一级所需的进位信息,无需等待所有低位的实际进位值逐级传递过来,大大提高了运算速度。
| ##container## |
|---|
 |
支持减法(补码)运算的ALU
| ##container## |
|---|
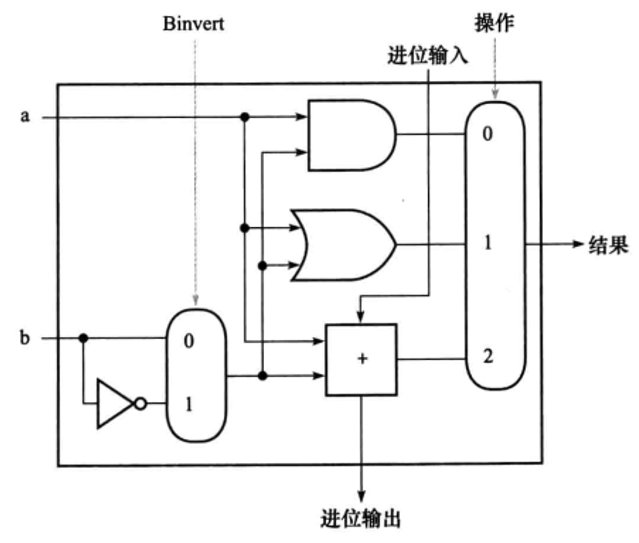 |
Tip
如果是减法, 那么 A - B = A + (-B), 则时候 就是 , 然后默认初始(第一个ALU)进位为1, 代表补码运算. (注, B 需要按位取反再加)

