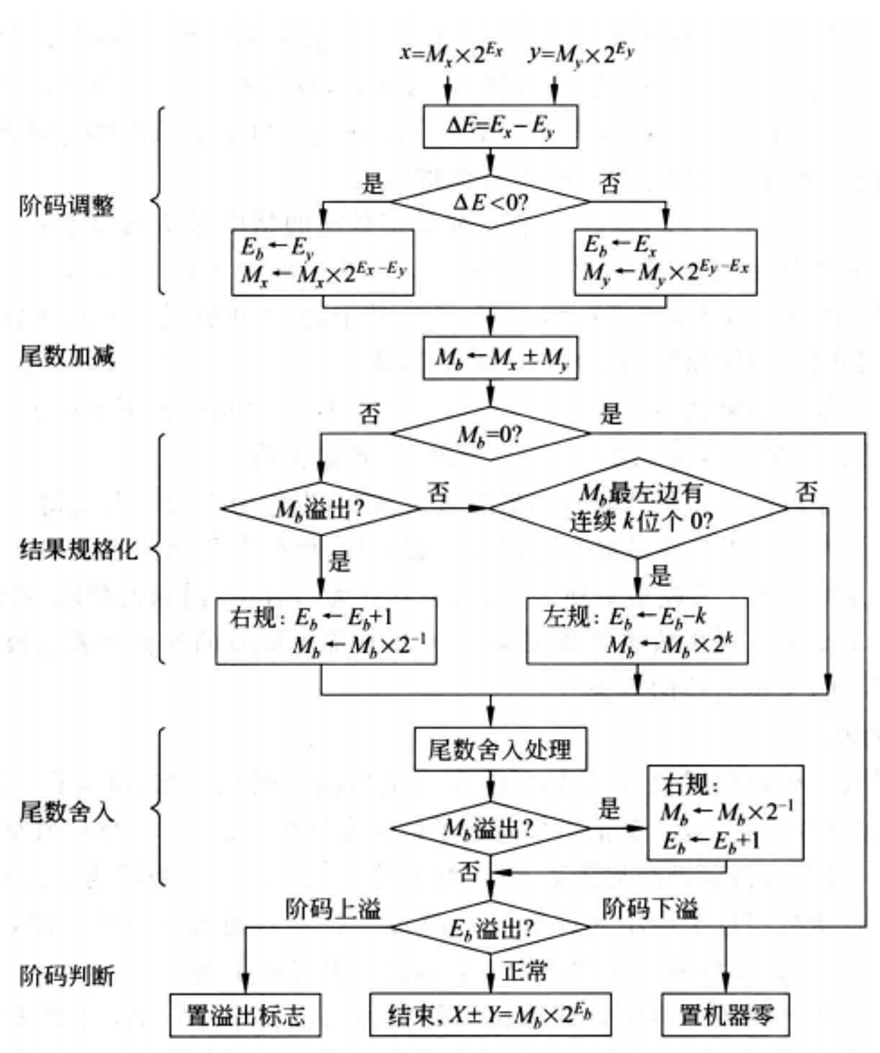
浮点数加减法
十进制的例子
不能将0.123和0.456直接相加,因为阶数不一样,要把阶数调整为相同(往大的调整)之后再相加。
- 结果的尾数为两个尾数之和,阶数为调整之后的阶数。
so,浮点数加减法运算其实很简单,总共就5步:
- 对阶、尾数运算、规格化、舍入、溢出判断。
为例,基于IEEE754标准
1. 对阶
Tip
使 和 的阶码相等, 以使尾数可以相加减。
原则: 小阶向大阶看齐, 阶小的那个数的尾数右移, 右移的位数等于两个阶(指数)的差的绝对值。
大多数机器采用IEEE754 标准来表示浮点数, 阶数为移码表示因此, 对阶时需要进行移码减法运算, 并且尾数右移时按原码小数方式右移, 符号位不参加移位, 数值位要将隐含的一位1右移到小数部分, 空出位补0。为了保证运算的精度, 尾数右移时, 低位移出的位不要丢掉,应保留并参加尾数部分的运算。
tips: 自己手算时直接用真值算即可
Tip
注: 移码 - 移码 != 移码, 而是 == 补码
证明: 记阶码为 在IEEE754 标准中其偏置值为 (n 为阶码位数), 现在有两个数的阶码的真值为
回顾:
- 补码的定义式:
Tip
注: 对于 两个移码 相加, 必需保证偏置值为 才满足: 移码 + 移码 != 补码
2. 尾数加减
对阶后两个浮点数的指数相等,可以进行对阶后的尾数相加减。
因为IEEE754采用定点原码小数表示尾数, 所以, 尾数加减实际上是定点原码小数的加减运算(与定点加减法一样)。
因为IEEE754浮点数尾数中有一个隐藏位, 所以,在进行尾数加减时, 必须把隐藏位还原到尾数部分。运算过程中, 在尾数右移时保留的附加位也要参加运算。
因此, 在用定点原码小数进行尾数加减运算时, 在操作数的高位部分和低位部分都需要进行相应的调整。
进行加减运算后的尾数不一定是规格化的, 因此, 浮点数的加、减运算需要进一步进行规格化处理。
3. 尾数规格化
Tip
左规、右规, 保证最高有效位为1
-
右规
-->: 尾数右移一位, 阶码加1。- 尾数右移时, 最高位1被移到小数点前一位作为隐藏位, 最后一位移出时, 要考虑舍入。阶码加1时, 直接在末位加1。
-
左规
<--: 数值位逐次左移, 阶码逐次减1, 直到将第一位1(隐藏位)移到小数点左边。
4.尾数的舍入处理
Tip
在对阶和尾数右规时, 可能会对尾数进行右移, 为保证运算精度, 一般将低位移出的位保留下来, 参加中间过程的运算, 最后再将运算结果进行舍入, 还原表示成IEEE 754格式。
-
保留多少附加位才能保证运算的精度?
IEEE754标准规定, 所有浮点数运算的中间结果右边都必须至少额外保留两位附加位。-
这两位附加位中, 紧跟在浮点数尾数右边那一位为保护位或警戒位(guard), 用以保护尾数右移的位;
-
紧跟保护位右边的是舍入位(round), 左规时可以根据其值进行舍入。
-
在
IEEE 754标准中, 为了更进一步提高计算精度, 在保护位和舍入位后面还引入了额外的一个数位, 称为粘位(sticky), 只要舍入位的右边有任何非0数字, 粘位就被置1; 否则, 粘位被置0。
-
-
IEEE754标准的舍入方法:- 舍 入。
- 朝 方向舍入。总是取右边最近可表示数, 也称为正向舍入或朝上舍入。
- 朝 方向舍入。总是取左边最近可表示数, 也称为负向舍入或朝下舍入。
- 朝 方向舍入。直接截取所需位数,丢弃后面所有位,也称为截取、截断或恒舍法。这种舍入处理最简单。对正数或负数来说,都是取更靠近原点的那个可表示数,是趋向原点的舍入,因此,又称为趋向零舍入。
5.溢出判断
在进行尾数规格化和尾数舍入时, 可能会对结果的阶码执行加、减运算。因此, 必须考虑结果的指数溢出问题:
-
若一个正指数超过了最大允许值(
127或1023), 则发生指数上溢, 机器产生异常, 也有的机器把结果置为 (数符为0时) 或 (数符为1时) 后, 继续执行下去。 -
若一个负指数超过了最小允许值(
-149或-1074), 则发生指数下溢, 此时, 一般把结果置为 (数符为0时)或 (数符为1时), 也有的机器引起异常。
溢出判断实际上是在上述尾数规格化和尾数舍入过程中进行的, 只要涉及阶码求和/差, 就可以在阶码运算部件中直接用溢出判断电路来实现。涉及阶码求和/差的情况有以下情况:
-
右规和尾数舍入。一个数值很大的尾数舍入时, 可能因为末尾加1而发生尾数溢出, 此时, 可以通过右规来调整尾数和阶。
右规时阶加 1, 导致阶增大, 因此需要判断是否发生了指数上溢。只有当调整前的阶码为
1111110, 加 1 后, 才会变成1111111而发生上溢;如果右规前阶码已经是
1111111, 则右规后变为0000000, 因而会造成判断出错。所以,
- 右规前应先判断阶码是否为全1, 若是, 则不需右规, 直接置结果为指数上溢; 否则, 阶码加 1, 然后判断阶码是否为全 1 来确定是否指数上溢。
-
左规。左规时数值位逐次左移, 阶码逐次减1, 所以左规使阶码减小, 故需判断是否发生指数下溢。
其判断规则与指数上溢类似,
- 首先判断阶码是否为全 0, 若是, 则直接置结果为指数下溢; 否则, 阶码减 1, 然后判断阶码是否为全 0 来确定是否指数下溢。
从浮点数加、减运算过程可以看出, 浮点数的溢出并不以尾数溢出来判断, 尾数溢出可以通过右规操作得到纠正。运算结果是否溢出主要看结果的指数是否发生了上溢, 因此是由指数上溢来判断的。
流程图总结
| ##container## |
|---|
 |
练习
-
用
IEEE 754单精度浮点数加减运算计算 。 -
[408考研真题的说] 设浮点数格式: 阶码尾数均用补码表示, 补码含两位符号位。阶码占5位尾数占7位, 没有隐藏位。
问 是否溢出?

