定点数除法
回顾: 十进制除法

我们知道, 商的位数最大是
二进制除法
二进制除法的运算,本质上相当于看最多几个除数累加能逼近于被除数。(加上余数后就等于被除数)。
可以通过减法和移位运算来实现。
- 无符号数除法
- 有符号数原码除法
- 有符号数补码除法
无符号数除法
除法只有两种可能性: 与 (0不能做除数)
-
先对除数末尾补零到与被除数位数对齐(通过左移实现),左移一位代表乘2,右移一位代表除2;
-
判断大小,确定该位商1还是商0。
不像人那样聪明,计算机不可能提前知道除数是否小于被除数。
先让被除数减去除数,若结果为>=0,说明被除数>=除数,直接商1。若结果为负数,说明被除数<除数,说明不能减,则先恢复被除数的原值,再商0。
以8位二进制94除以4为例:
Tip
注: 除数左移4位, 的4是因为 8位被除数 - 4位除数 + 1 = 5, 而左移0位 对于 1, 所以移动4.
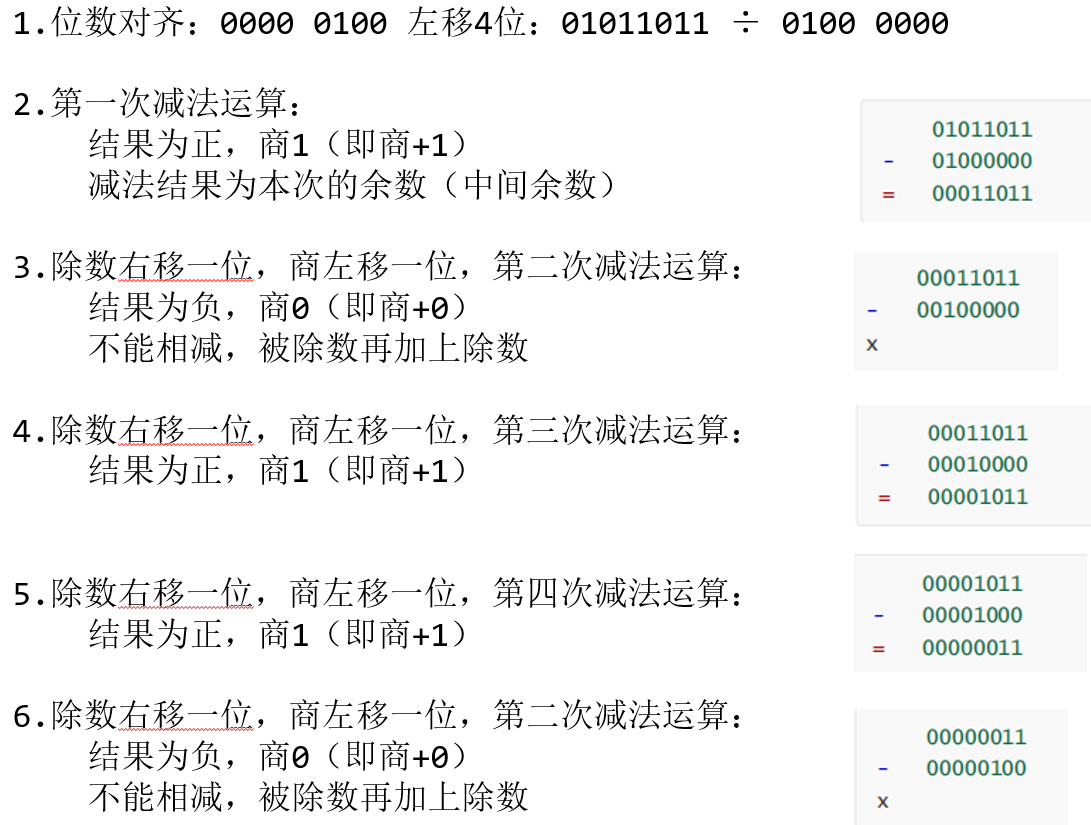
可能的过程代码:
#include <cstdio>
// 有 O(1) 得到二进制长度的方法
int getBitLen(int x) {
int res = 0;
while (x) {
++res;
x >>= 1;
}
return res;
}
// a / b && a >= b
int divisionByBit(int a, int b) {
int len = getBitLen(a) - getBitLen(b);
b <<= len;
int quotient = 0; // 商
while (len--) {
if (a - b >= 0) {
quotient |= 1;
a -= b;
}
quotient <<= 1;
b >>= 1;
}
// 第 len + 1 次, 并且不需要移位了
if (a - b >= 0) {
quotient |= 1;
a -= b;
}
printf("mod: %d\n", a); // 余数
return quotient;
}
int main() {
printf("%d\n", divisionByBit(21, 4)); // 4
return 0;
}
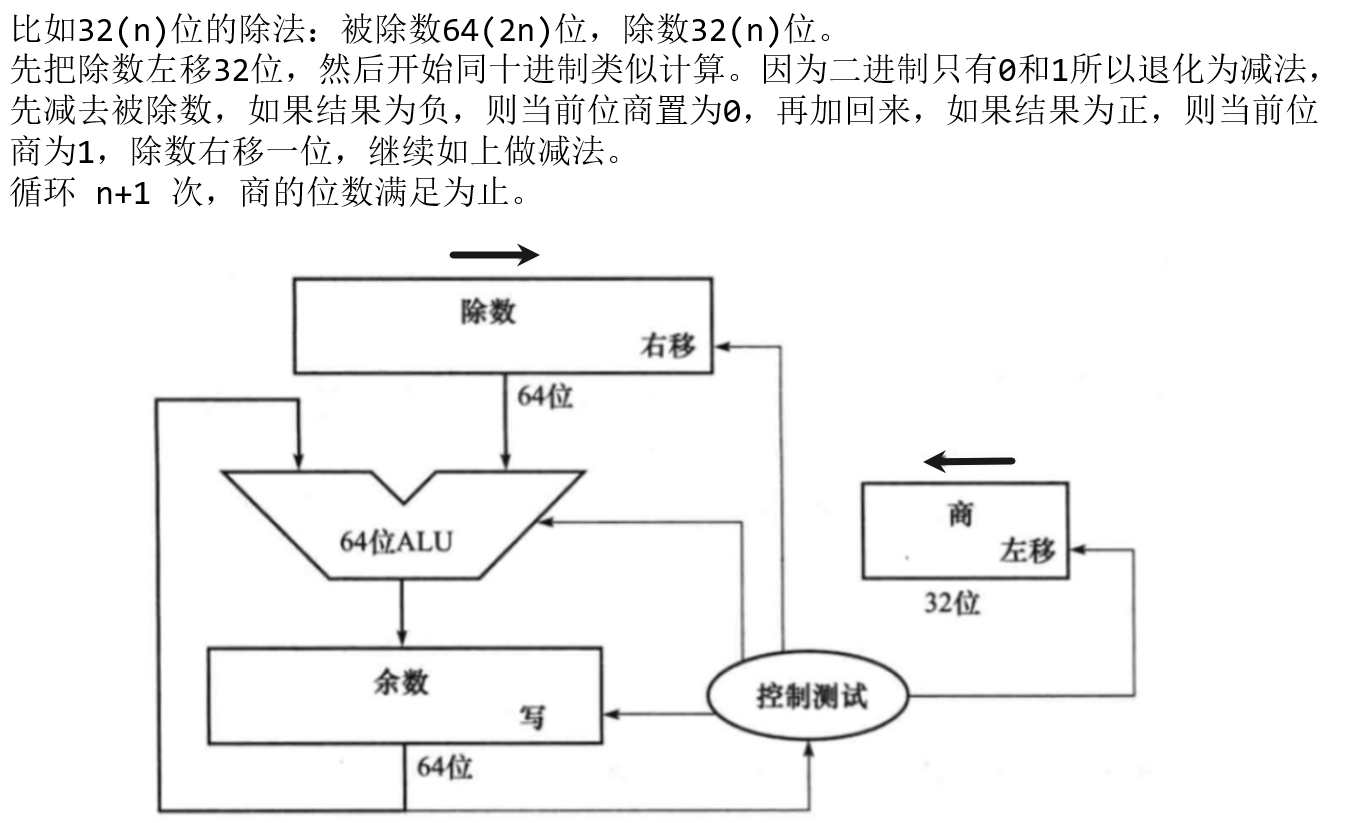
电路图
| ##container## |
|---|
 |
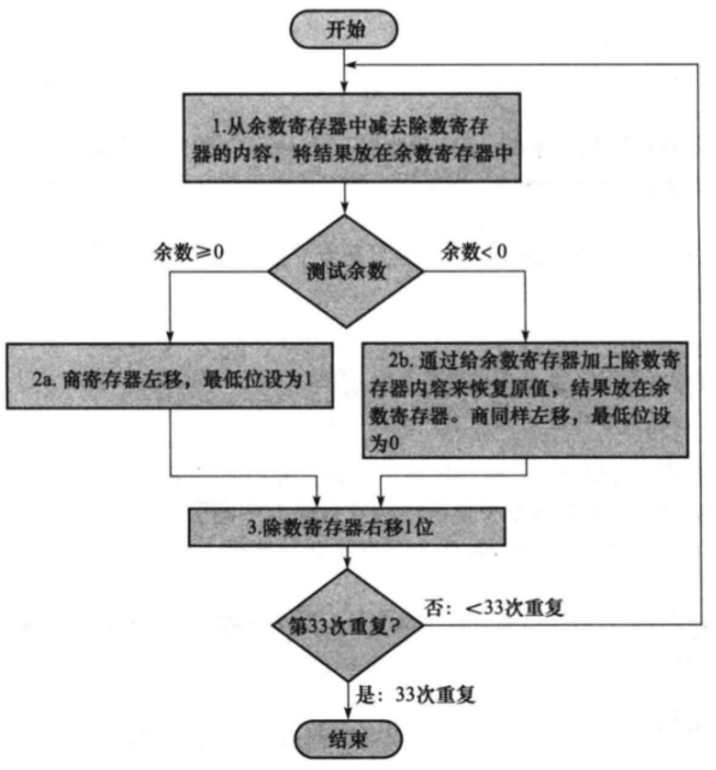
流程图
| ##container## |
|---|
 |
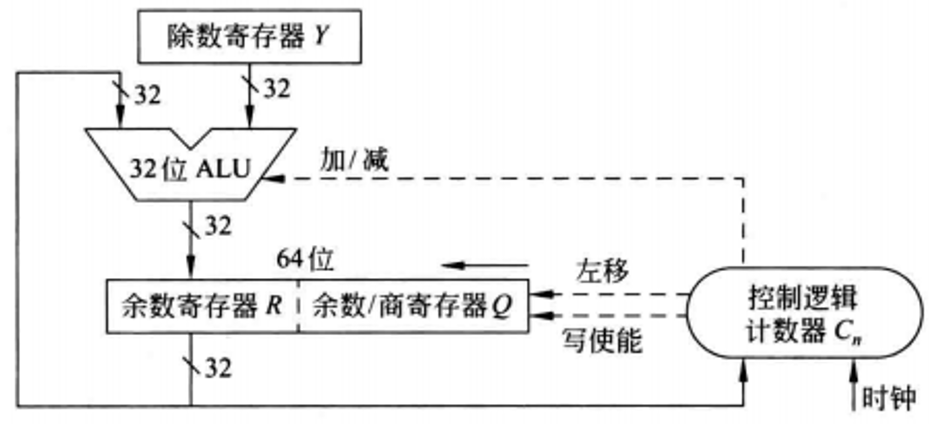
电路图-优化
当然,除法器也可以做进一步的优化。
- 加速方法就是通过将源操作数和商移位与减法同时进行。
| ##container## |
|---|
 |
有符号数原码除法
商的符号位与数值位分开来求
-
符号位: 被除数和除数的符号位
异或运算得到 -
数值位: 被除数和除数的数值位执行
无符号除法
有符号数补码除法
符号位参与运算,除数和被除数,余数和商均用补码表示。符号拓展。
其他过程与 无符号除法一致。
区别在于判断是否可以减时,不能直接相减看结果的符号位,要按分情况来看
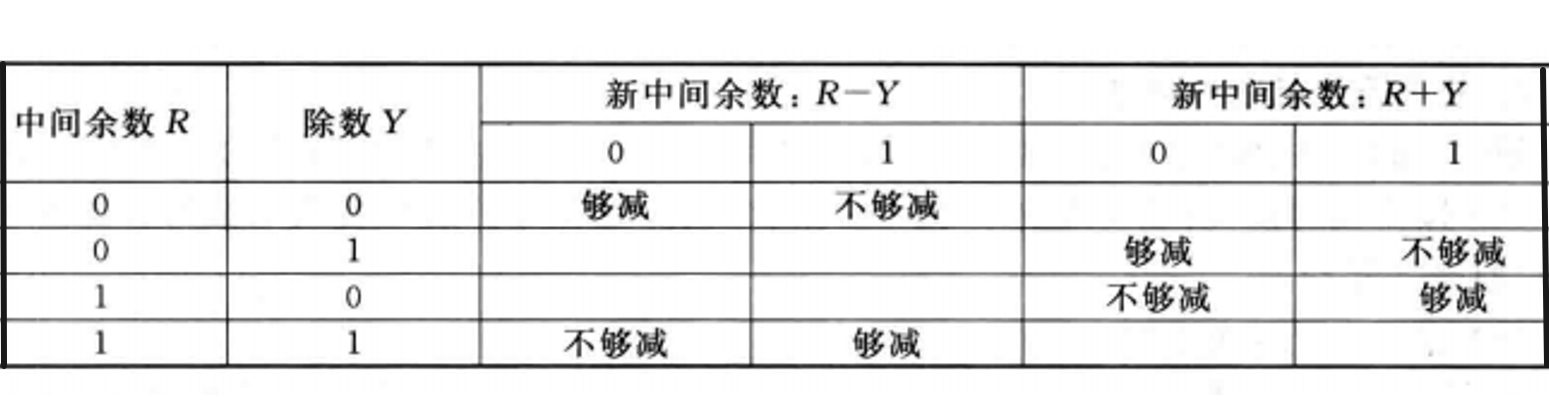
留坑: 不恢复的补码除法
我们之前讲的都是减后判断符号位再决定, 并且商0还需要恢复.
但是实际上现在我们都是用不恢复的做法, 但是可能比较复杂, 因此留坑.

