中位数贪心

问题

在一个一维数轴上, 分布有 n 个商店, 现在需要定一个货仓的位置, 使得货仓到所有的商店的距离的和最小 (因为考虑到燃油等经济问题...), 请问货仓应该建造在哪里?

证明

不妨设如下场景 A ~ G 代表商店, H 代表货仓

  A      B          C        D  E    F       G
----------------------------------------------> x
C++

不妨先随便给货仓一个位置先:

  A      B          C        D  E    F       G
----------------------------------------------> x
    H
C++

如果此时 H 先左移动 1 个单位, 那么它与 A 的距离 - 1, 而与 B ~ G 的距离 + 1 (显然距离和变大了)
如果此时 H 先右移动 1 个单位, 那么它与 A 的距离 + 1, 而与 B ~ G 的距离 - 1 (显然距离和变小了(因为距离减的数量 > 距离加的数量))
由上就可以发现: 如果距离减的数量 > 距离加的数量那么距离和就会减少
- 所以我们继续往右移动移动移动...

  A      B          C        D  E    F       G
----------------------------------------------> x
    --> --> --> --> --> -->  H
C++

当 距离减的数量 == 距离加的数量 时, 即上面这种情况, 则为最佳位置(距离的和最小位置), (因为往左那么距离减的数量 < 距离加的数量, 往右也是距离减的数量 < 距离加的数量)

所以就得出中位数贪心这个东西, 寻找的是距离的和最小并且没有限制, 所以是贪心, 而最终结果是在中间这个仓库上, 所以称为中位数.

如果商店的数量不是奇数, 而是偶数呢?

  A      B      C      D     E       F  G  Z
----------------------------------------------> x
                          H
C++

还是中间, 不过是 [D, E] 位置之间.

何故なら, 「当距离减的数量 == 距离加的数量时, 满足距离的和最小位置」からである.

而在 [D, E] 位置之间正好满足 距离减的数量 == 距离加的数量, 所以直接选择在 D 或者 E 也是没问题的.

转化为代码

对于一个数组 arr, 其值只会为0或1, 记1是商店. 请在数组中选择一个index作为仓库的位置使得其到最近的 num 个商店的 距离和最小(对于arr[m] = 1, index到arr[m]的距离为abs(index - m)(即索引的差)).

由上面的偶数证明可以知道, 不一定选择0的位置才会使得距离和最小.
所以把全部值为1的arr[i]的索引记录到tmp数组中, 以减少遍历次数.

##container##
代码原理解释图

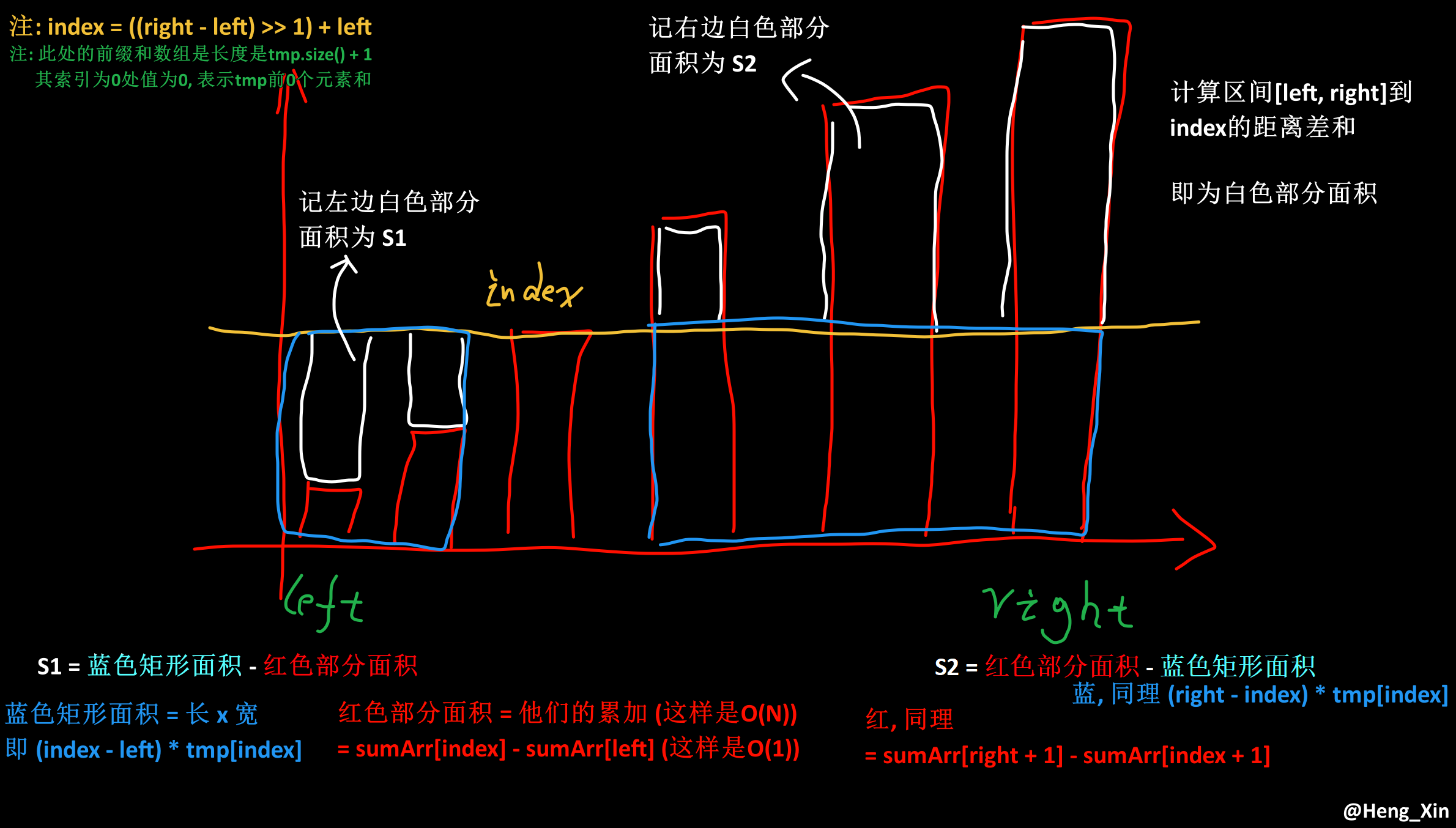注: 一定要保证tmp数组的值是从小到大排序的!

class Text {
    int minDistanceSum(vector<int>& tmp, vector<int>& sumArr, int left, int index, int right) {
        int s1 = (index - left) * tmp[index] - (sumArr[index] - sumArr[left]);
        int s2 = (sumArr[right + 1] - sumArr[index + 1]) - (right - index) * tmp[index];
        return s1 + s2;
    }
    
public:
    int getMinDistanceSum(vector<int> arr, int num) {
        vector<int> tmp;
        for (int i = 0; i < arr.size(); ++i) {
            if (arr[i]) {
                tmp.push_back(i);
            }
        }

        // 计算前缀和 注意, 是 sumArr 下标为 [1] 对应 tmp[0]
        int n = tmp.size();
        vector<int> sumArr(n + 1);
        for (int i = 0; i < n; ++i)
            sumArr[i + 1] = sumArr[i] + tmp[i];

        // 计算 index 到 num 个 商店 距离和最小 (从 右边界开始算, 防止越界)
        int res = 1e9;
        for (int r = num; r < n; ++r) {
            int l = r - num;
            int index = ((r - l) >> 1) + l;
            res = min(res, minDistanceSum(tmp, sumArr, l, index, r));
        }
        return res;
    }
}
C++

问题​

证明​

转化为代码​

相关题目​

问题

证明

转化为代码

相关题目