力扣Hot100速记
最近打算把 Hot100 给它肝了, 不过只是每日3题罢了...
有些题目二刷了, 之前会的, 现在还是得思考, 但是这种东西, 你思考你就输了...
故本博客会记录题目, 并且把题目的解法总结为短短的几句话或者图示, 以方便我复习 =-=
长期更新 2025-05-10 15:05:03 から; 最近更新: 2025-10-11 22:40:46
1. 哈希
-
前缀和 (维护右枚举左), 秒了
-
给每一个字符串排序后哈希加入分组, 然后再return; , 是字符串长度
进阶的是使用
array<int, 26>来记录数字然后哈希;更厉害的是使用质数表然后乘法, 这样可以直接拿数字哈希
-
在未排序的数组中, 找到最长连续序列, 使用哈希集合, 枚举 与 来不断 next; 维护最大长度, 剪枝就是先把全部数先放集合, 从而去重; 然后再判断 是否在集合, 如果在, 说明之前已经枚举过它了, 不会有更长的, 可以直接
continue了
2. 双指针
-
一个指针指向数字的后一个位置, 和一个不断变量的数字, 如果非0, 就和该指针交换位置, 并且指针++;
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int mae = 0;
for (int& x : nums) {
if (x) {
swap(x, nums[mae]);
++mae;
}
}
}
}; -
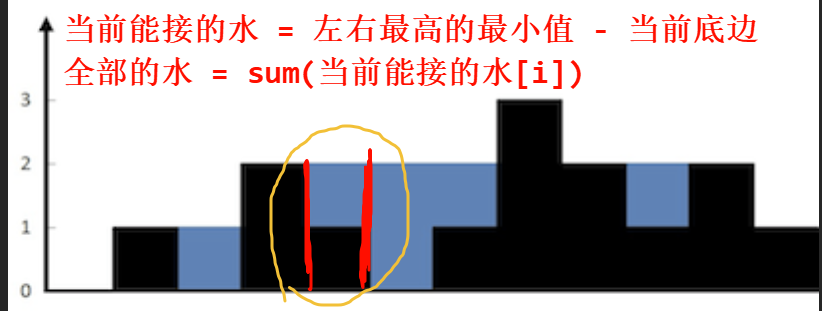
左右指针, 维护最高的柱子, 同时遍历过程中, 不断计算并维护当前的水的最大值; 移动左右的低的柱子
-
有很慢的 的哈希的维护右枚举左的写法.
正解应该是排序后双指针
class Solution {
using ll = long long;
public:
vector<vector<int>> threeSum(vector<int>& nums) {
// 和为 0 的, 不重复的 (v1, v2, v3)
int n = nums.size();
vector<vector<int>> res;
ranges::sort(nums); // 排序后, 定一, 然后就是 [有序版-两数之和]
for (int i = 0; i < n - 2; ++i) {
int v = nums[i];
if (i && v == nums[i - 1]) // 去重
continue;
if (v + nums[i + 1] + nums[i + 2] > 0) // 剪枝: 当前 + 最小 > 0 => 不可能会 == 0
break;
if (v + nums[n - 1] + nums[n - 2] < 0) // 剪枝: 当前 + 最大 < 0 => 目前不会 == 0
continue;
int l = i + 1, r = n - 1, tg = -v;
while (l < r) {
int x = nums[l] + nums[r];
if (x > tg) {
--r;
} else if (x < tg) {
++l;
} else { // ==
int lv = nums[l], rv = nums[r];
res.push_back({v, lv, rv});
while (l < r && lv == nums[l]) // 去重
++l;
while (l < r && rv == nums[r]) // 去重
--r;
}
}
}
return res;
}
}; -
前缀和 + 后缀和 罢了 (其中一个方法)
3. 滑动窗口
-
哈希表计数 + 滑窗 即可
-
哈希表计数字母 + 滑窗
4. 子串
-
前缀和上的两数之和 (可维护右枚举左, 记得写等式推: , 其中 为前缀和的值)
-
单调双端队列: {维护单调性 => 元素离开窗口 => 记录答案} for in nums 即可~
-
哈希计数字符个数 + 触发阈值的滑窗 (如果满足字符了 => 才开始减)
class Solution {
public:
string minWindow(string s, string t) {
auto hash = [](char c) -> int {
return (c & ' ') ? c - 'a' : c - 'A' + 26;
};
array<int, 26 + 26> cntS{}, cntT{};
for (char c : t)
++cntT[hash(c)];
int n = s.size(), isOk = [&]{
int res = 0;
for (int v : cntT)
res += v > 0;
return res;
}();
int resBegin = 1e9, resLen = 1e9;
for (int i = 0, l = 0; i < n; ++i) {
int idx = hash(s[i]);
if (++cntS[idx] == cntT[idx])
--isOk;
while (!isOk) {
int jdx = hash(s[l]);
if (cntS[jdx]-- == cntT[jdx]) {
++isOk;
if (resBegin == (int)1e9 || i - l + 1 < resLen)
resBegin = l, resLen = i - l + 1;
}
++l;
}
}
return resBegin == (int)1e9
? ""
: s.substr(resBegin, resLen);
}
};
5. 普通数组
-
贪心/dp: 如果小于0, 就不选了, 然后维护这个过程中的最大值
-
排序后, 从头遍历, 看看是否答案的右端点是否 大于 当前的左端点, 如果是则 更新当前答案的右端点的最大值, 如果否, 则答案新增一个区间
-
如果不想额外空间, 那么就上结论吧: 答案 = 反转整个数组 + 反转 [0, k) + 反转 [k, n)
@todo: 有空把推导深入看看, 我用的是交换法, 有点难调, 发现答案是 gcd(k, n) 轮交换... 不是同一个算法吧~
-
返回的数组做后缀积, 然后顺序再一次前缀积即可
-
换座位: 假设 [1, n] 都在自己座位上, 如果 nums[i] 不在 i + 1 上, 说明位置不对, 给她换了:
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n; ++i) {
// 在 [1, n] 内
// nums[i] - 1 是因为索引从 0 开始
// nums[nums[i] - 1] == nums[i]
// 的前提是 nums[i] = i + 1
while (nums[i] >= 1
&& nums[i] <= n
&& nums[nums[i] - 1] != nums[i]
) {
// 交换: 把这里的换过去, 那里的也换过来
swap(nums[i], nums[nums[i] - 1]);
}
}
for (int i = 0; i < n; ++i) // 最终判断第一次 nums[i] != i + 1 的
if (nums[i] != i + 1) // 就是缺少 i + 1 号同学
return i + 1;
return n + 1; // 否则就是都有; 缺 n + 1
}
};
6. 矩阵
-
把第一行和第一列作为标志位, 再另外使用两个变量标记第一行、列本身是否有0即可
-
定义方向变量, 绕边内入, 当越界或者走过了, 就可以换方向了.
-
数学本质: 两次翻转等于一次旋转
- 竖着看: 第 列的东西去了 第 行
- 横着看: 第 行的东西去了 第 列
故, 矩阵按照主对角线翻转,
把每一行翻转,
-
斜着看, 就是一颗二叉搜索树
7. 链表
-
结论: 让先到末尾的继续从另一个的开始走, 这样 n + m + l 等距离. 并且都为交点处.
-
边走边反转,
tmp -> mae -> (node)=>tmp <- mae -> (node) -
时间 + 空间解法: 查找中间节点 (快慢指针) + 反转链表 后, 双指针
-
题意仅 找环: 快慢指针, 如果相等就有环. 找到 nullptr 显然无环.
-
暴力: 上
unordered_set<Node*>正解: Floyd 判圈算法, 记忆: 双指针相遇后, 慢指针和头指针再走 a 步相遇点为入环点.
推导: 记 , , 那么当慢指针走了 步快慢指针 相遇时候, 快指针走了 步.
假设 快指针比慢指针多走了 圈, 那么此时它们走过 , 即 距离.
而慢指针在 环内 总共走了: , 即 到达相遇点.
说明, 从相遇点, 再走 步, 就是入环口了, 即 , 即 .
为什么呢? 就类似于从入环口跑 圈, 最后还是回到入环口.
-
没什么好说的, 就双指针然后比对看着选
-
模拟, 记录一下进位即可.
-
使用 虚拟头节点 (避免情况讨论), 然后双指针从虚拟头节点开始, 快指针先走 n 步. 然后一起走, 等到头了, 慢指针就是要删除的.
-
使用虚拟头节点, 然后
while (node && node->next && node->next->next)并且依次把上上个节点上一个节点当前节点列好, 你画图就清晰了!



